Question

Скорость точки, движущейся
прямолинейно, задана уравнение
v = t^2 − 8t + 2.
Вычислите е путь за 2с от начала
движения

даю 60 баллов

Answer 1

   Известно, что скорость — производная перемещения по времени. Следовательно, чтобы идти обратно, нужно интегрировать. Интеграл будет определённый, с пределами [0;2], так как просят найти перемещение за первые 2 секунды. Важно! Если необходимо найти перемещение — ищем определённый интеграл, а если путь, то площадь под графиком:

$\displaystyle{ \frac{d{\ell}}{dt} }={v}(t)$

Умножаем обе части на dt:

$\displaystyle{ {d{\ell}} }={v}(t)dt$

Интегрируем:

$\displaystyle{ {\ell} = \int\limits^2_0 {{v}(t)} \,dt }$

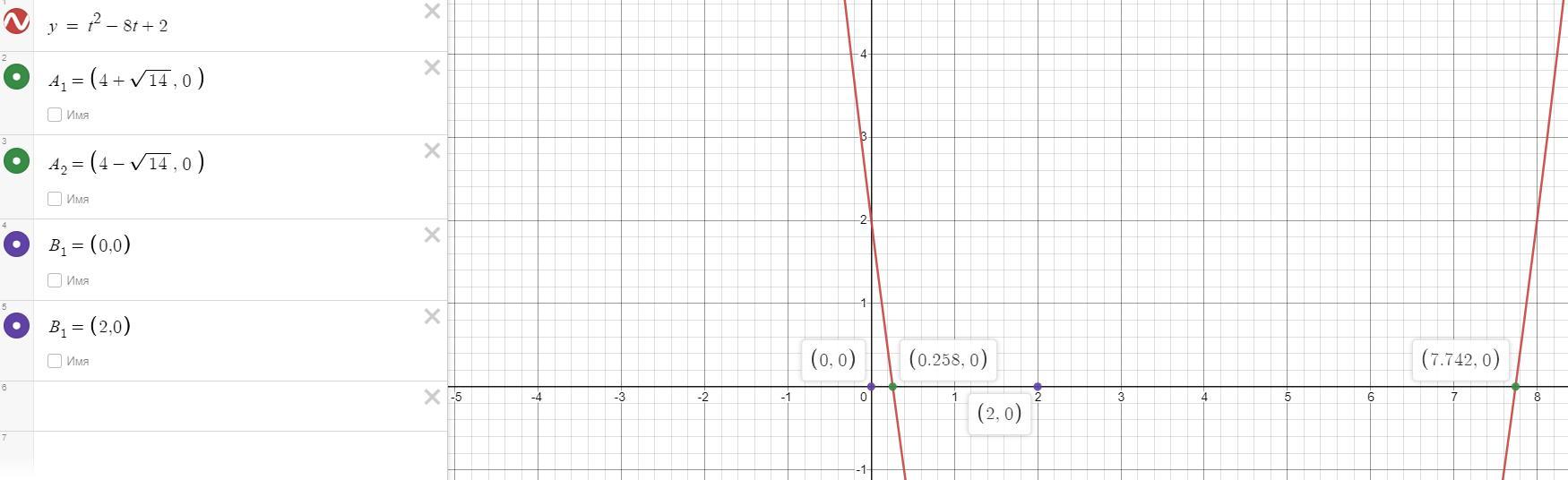
   Закон изменения скорости дан по условию. Найдём нули этой функции:

$t^2 - 8t+ 2 = 0$

$\displaystyle \left \{ {{ t_1 = 4+\sqrt{14} } \atop { t_2 = 4-\sqrt{14} }} \right.$

См. фото

Площадь в промежутке [0; 4 - √(14)] обозначим S1, а [4 - √(14); 2] - S2

$\displaystyle S_1 = | \int\limits^{4-\sqrt{14} }_0 t^2 - 8t+ 2 \, dt |$

$\displaystyle S_1 = | \frac{t^3}{3} - 4t^2 +2t | \Bigg{|}^\lims{4-\sqrt{14}}_{0}$

$\displaystyle S_1 = |\frac{28\sqrt{14} - 104}{3} | = \frac{28\sqrt{14} - 104}{3}$

$\displaystyle S_2 = | \int\limits^{2} }_{4-\sqrt{14}} t^2 - 8t+ 2 \, dt |$

$\displaystyle S_2 = | \frac{t^3}{3} - 4t^2 +2t | \Bigg{|}^\lims{2}_{4-\sqrt{14}}$

$\displaystyle S_2 = |\frac{76-28\sqrt{14} }{3} | = \frac{28\sqrt{14} - 76 }{3}$

Общая площадь:

$\displaystyle S_1 +S_2 = \frac{56\sqrt{14} - 180}{3}$