Предмет: Алгебра,
автор: Аноним
Помогите пожалуйста решить, нужно найти производную
Приложения:
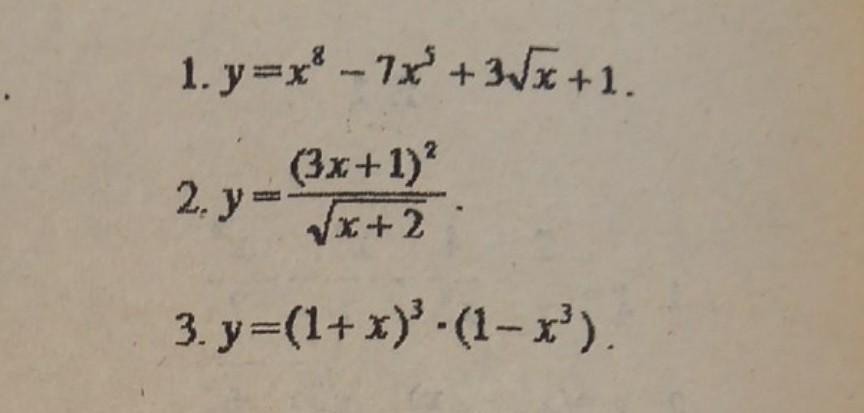
vnesen5571:
Ну там по идеи надо все плюсывать а потом умнажать?.
Ответы
Автор ответа:
1
Ответ:
Объяснение:
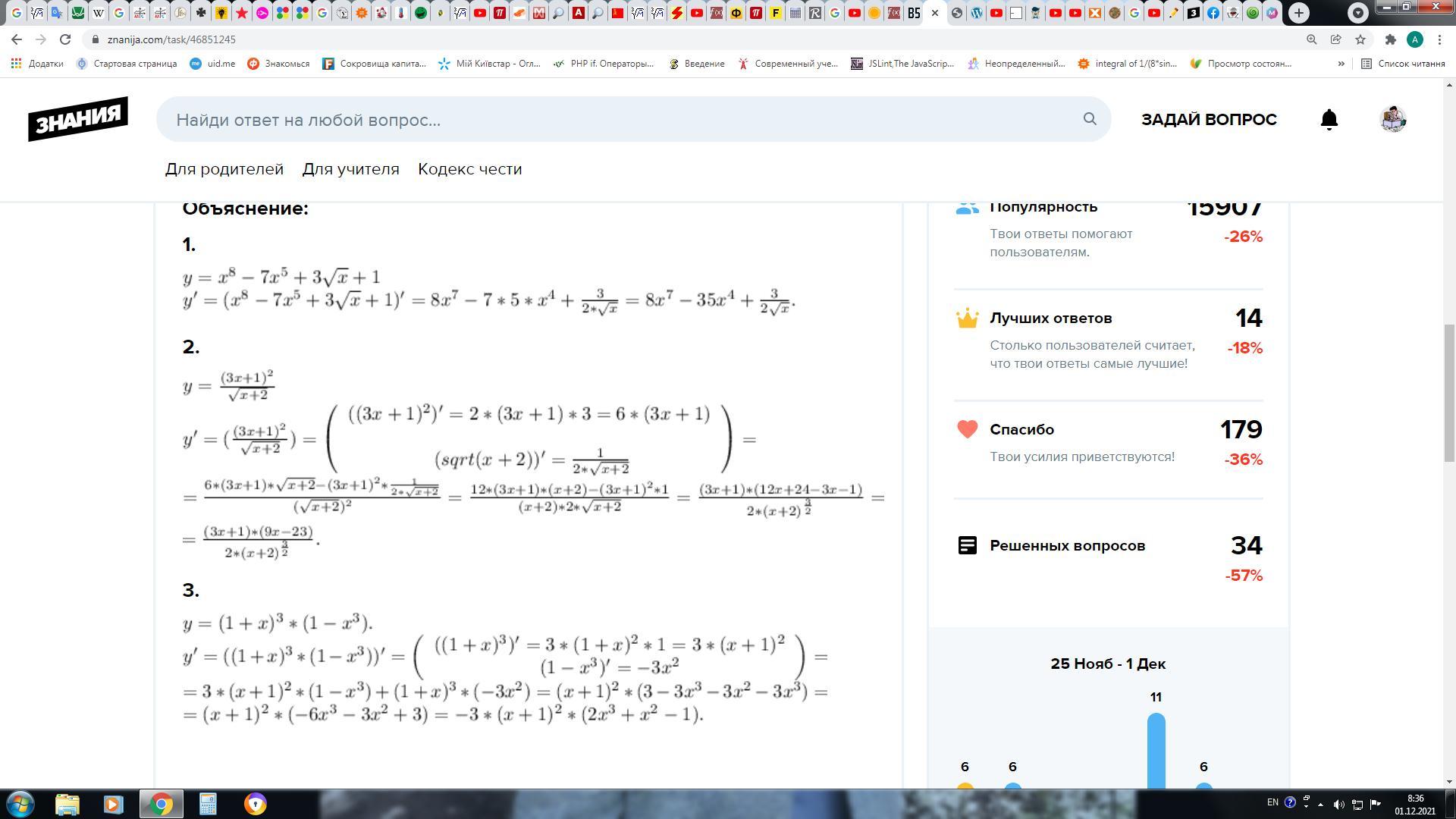
1.
2.
3.
Приложения:
Похожие вопросы
Предмет: Другие предметы,
автор: danillip
Предмет: Русский язык,
автор: katyha101
Предмет: Английский язык,
автор: Аня01928374651
Предмет: Биология,
автор: allamelisa1980
Предмет: Алгебра,
автор: lena733958