Предмет: Алгебра,
автор: Аноним
Помогите пожалуйста решить, нужно найти производную
Приложения:
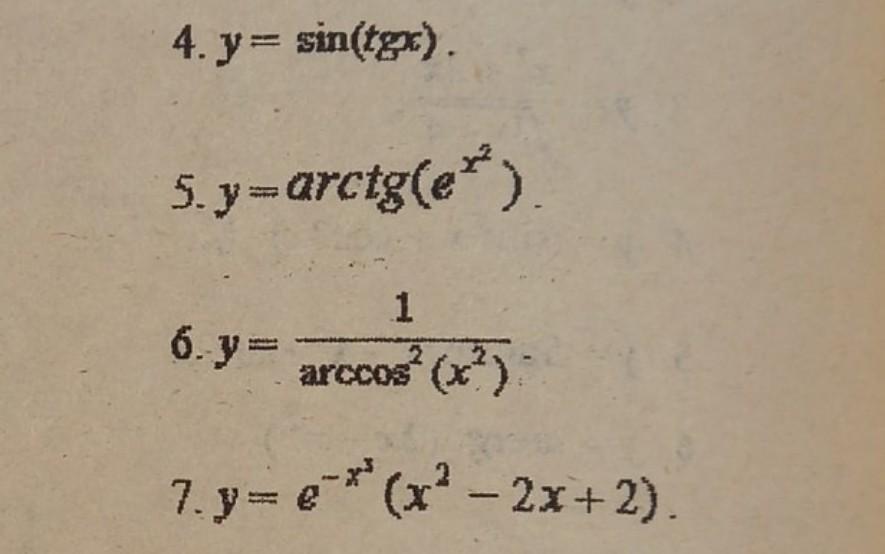
Ответы
Автор ответа:
0
Ответ:
Объяснение:
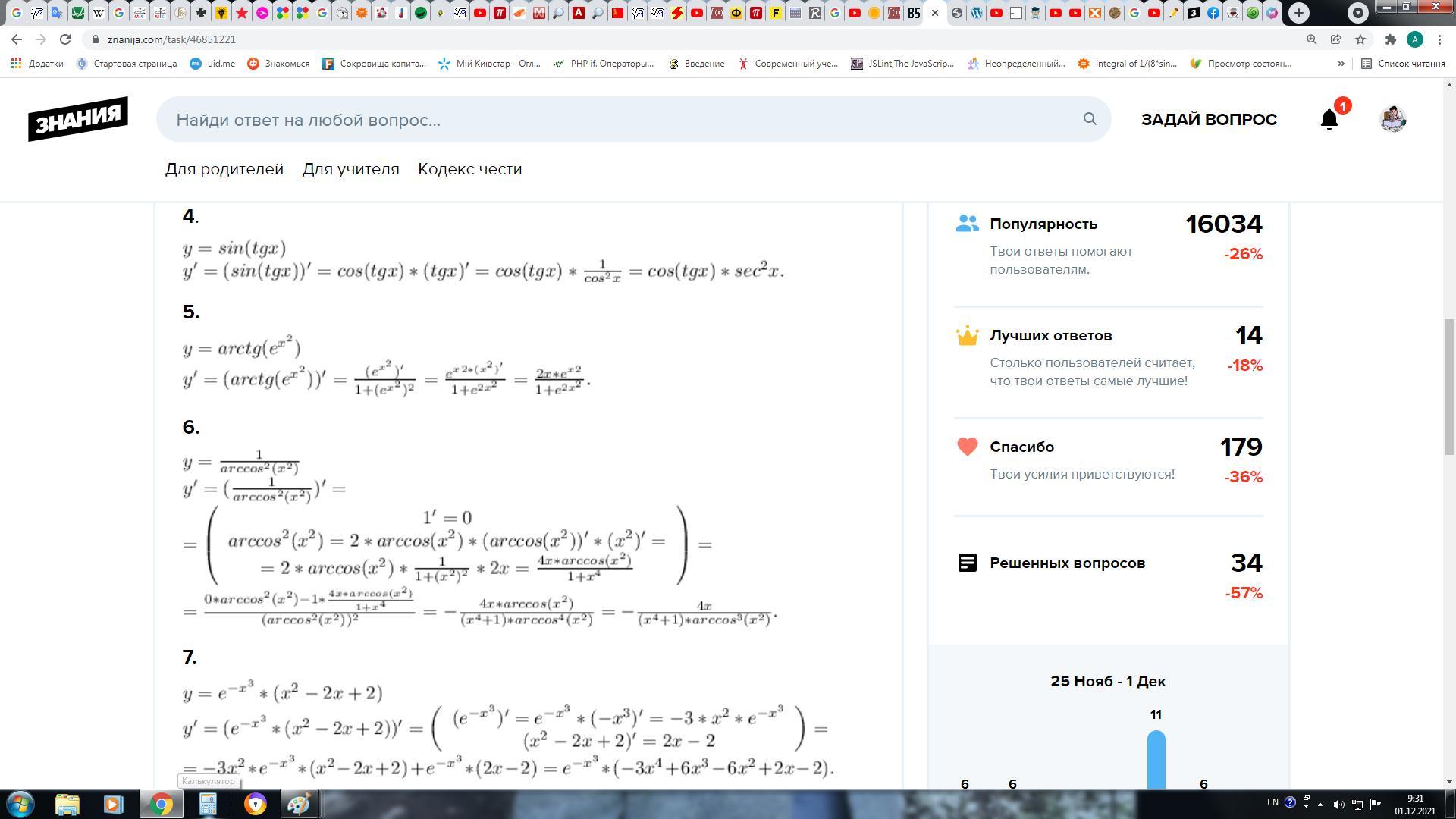
4.
5.
6.
7.
Приложения:
sangers1959:
Такой скриншот?
Похожие вопросы
Предмет: Английский язык,
автор: Аня01928374651
Предмет: Русский язык,
автор: Анастасия7202
Предмет: Русский язык,
автор: HappyCloyd
Предмет: Математика,
автор: максим13372288
Предмет: Алгебра,
автор: 2283411