Предмет: Геометрия,
автор: palmariukkatia
Точка О- центр кола, описаного навколо трикутника ABC (AB= AC). Знайти кути трикутника ABC, якщо кут BOC =32°. Скільки розв'язків має задача?
хелп ми плиииис
Ответы
Автор ответа:
2
Ответ:
Объяснение:
AB= AC =>△ABC - равнобедренный.
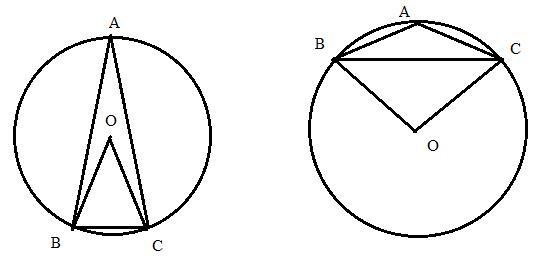
1) Равнобедренный треугольник с острым углом при вершине. <BOC=32° - центральный угол, опирающийся на малую дугу ВС=32°, а опирающийся на неё вписанный угол <BAC=32/2=16°. Тогда углы при основании <ABC=<ACB=(180-16)/2=82°
2. Равнобедренный треугольник с тупым углом при вершине. Центр окружности лежит вне треугольника. <BOC=32° - центральный угол, опирающийся на малую дугу ВС=32°. Угол <BAC - вписанный, опирается на большую дугу ВС=360-32=328° => <BAC=328/2=164°. Тогда углы при основании <ABC=<ACB=(180-164)/2=8°
Приложения:
Похожие вопросы
Предмет: Қазақ тiлi,
автор: Vlad1sLav69
Предмет: Русский язык,
автор: оооо69
Предмет: Окружающий мир,
автор: костя341
Предмет: Русский язык,
автор: sofiyashiman
Предмет: Литература,
автор: kikiolovue