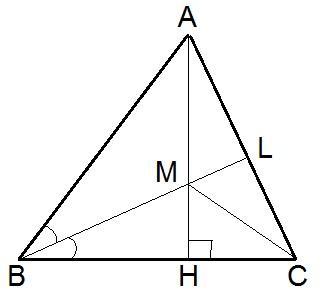
Высота АН и биссектриса BL остроугольного треугольника АВС пересекаются в точке М. Известно, что угол ВАН равен 22°, а угол ВCA равен 56°. Найдите угол АСМ. Ответ запишите в градусах, единицы измерения не указывать.
Ответы
Ответ: <ACM =34
Объяснение: Дано. <ВСА = 56°; <ВАН = 22°. АН⊥ВС; ВL - биссектриса <B.
Найти <ACM
См. рисунок. Так как АН⊥ВС (по условию), то ΔАНС - прямоугольный и <НАС = 180 - 90 - <BCA = 180-90-56 = 34. < BAC = <НАС + <BAH = 34 + 22 = 56. Таким образом, <ВАС = < ВСА = 56 . Следовательно Δ АВС - равнобедренный с основанием АС. В равнобедренном треугольнике биссектриса проведенная из вершины треугольника является и высотой и медианой. Следовательно, ВL⊥ АС и AL = LC. Так как ВL - высота и медиана в Δ АВС, то она является и высотой и медианой в Δ АМС, так как проходит через точку М. Но так как AL = LC, то Δ АМС - равнобедренный с раными сторонами АМ и МС. В равнобедренном треугольнике углы при основании равны. Значит <MAL = < MCL. Но, <MAL = <НАС = 34. Следовательно и < MCL = 34 и равен <ACM