Предмет: Алгебра,
автор: Аноним
нужно найти производную, помогите пожалуйста
Приложения:
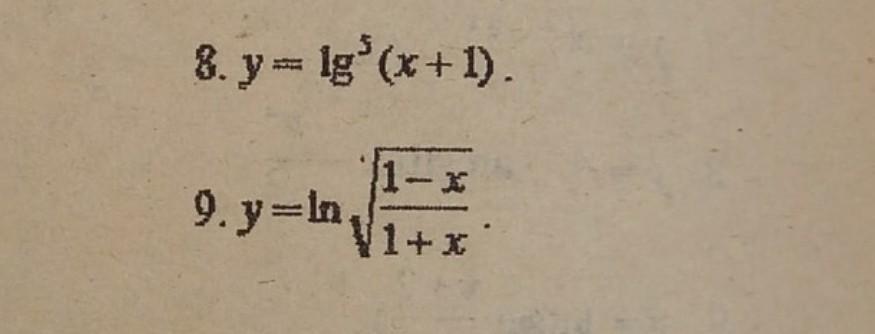
Ответы
Автор ответа:
1
8.
9.
Замечание. При преобразовании логарифма дроби в разность логарифмом мы написали модули, чтобы не сузить область определения. В дальнейшем модули исчезли, поскольку
Если Вам такую формулу не давали, Вы с легкостью можете ее вывести, рассматривая два случая раскрытия модуля. Впрочем, можно было модулей избежать, если использовать область определения логарифма:
Похожие вопросы
Предмет: Окружающий мир,
автор: маришка114
Предмет: Русский язык,
автор: рам9
Предмет: Окружающий мир,
автор: altfox
Предмет: Математика,
автор: Lyna4565
Предмет: Математика,
автор: hasl7