Предмет: Алгебра,
автор: Аноним
Помогите пожалуйста решить
Приложения:
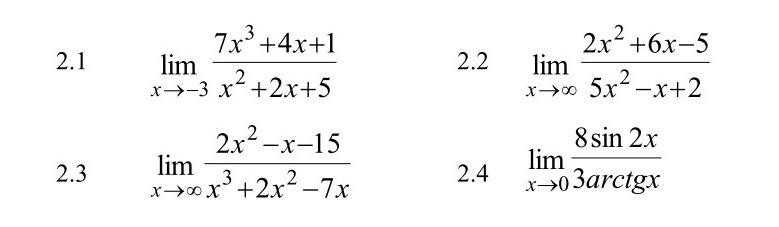
Ответы
Автор ответа:
1
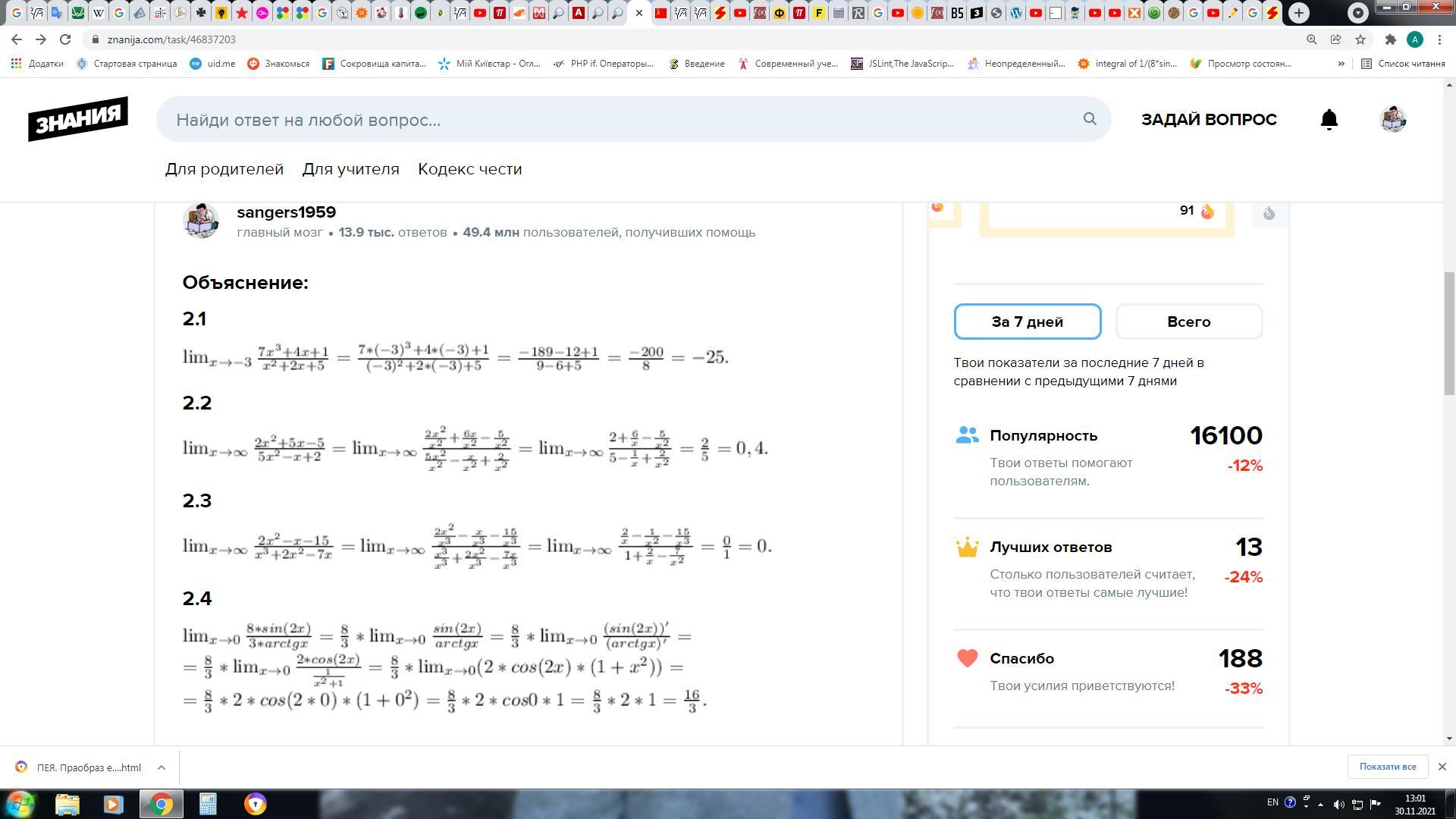
Объяснение:
2.1
2.2
2.3
2.4
Приложения:
sangers1959:
Удачи.
Автор ответа:
0
Ответ:
Объяснение:
!!!!!!!!!!!!!!!!!!!!!
Приложения:
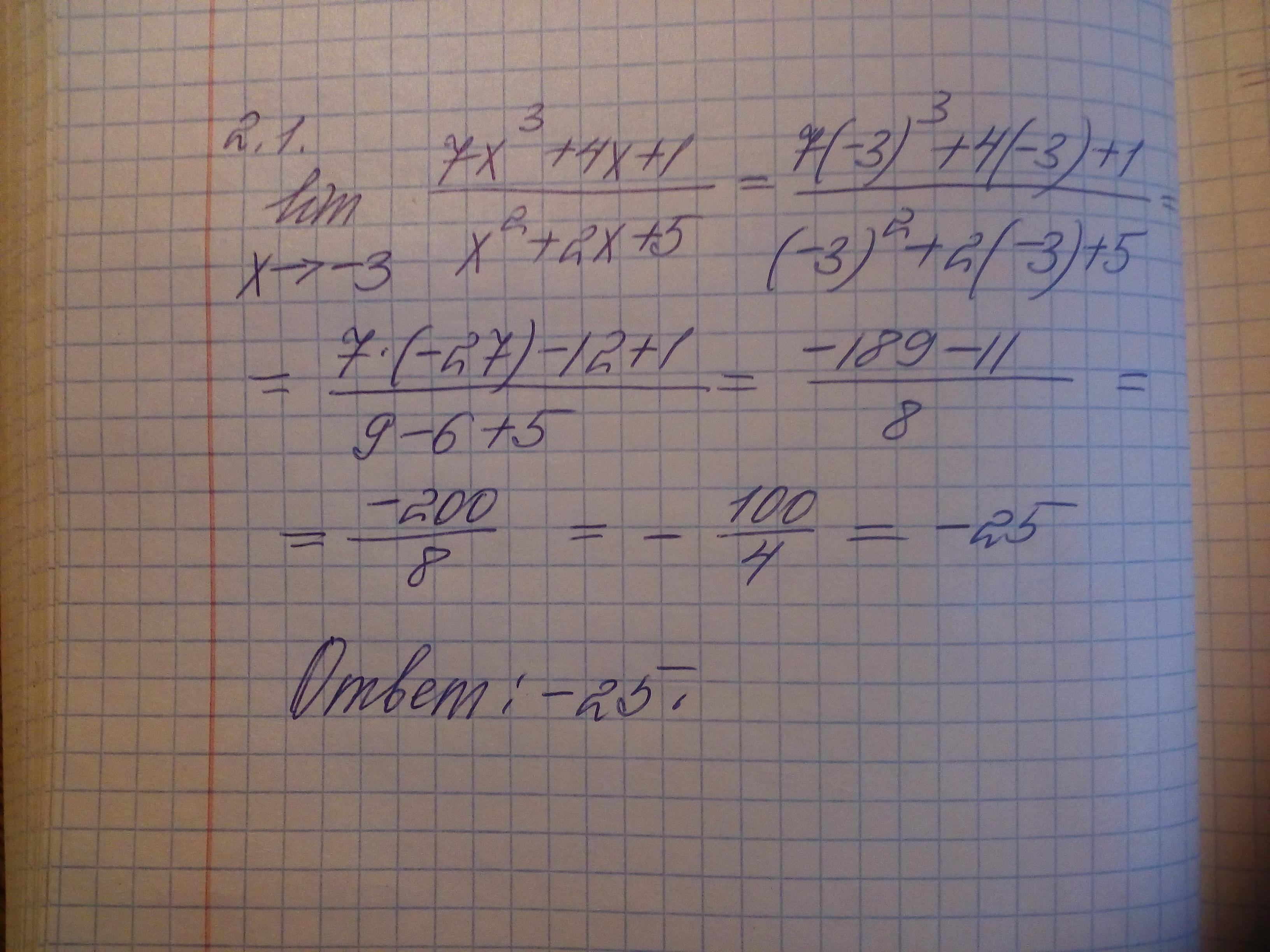



Похожие вопросы
Предмет: Русский язык,
автор: Karamelkin4444555555
Предмет: Русский язык,
автор: 2314669491
Предмет: Русский язык,
автор: карилл
Предмет: Английский язык,
автор: Аноним