Предмет: Алгебра,
автор: anik200579
алгебра номер 4,5 помогите просьба не знаете не пишите
Приложения:
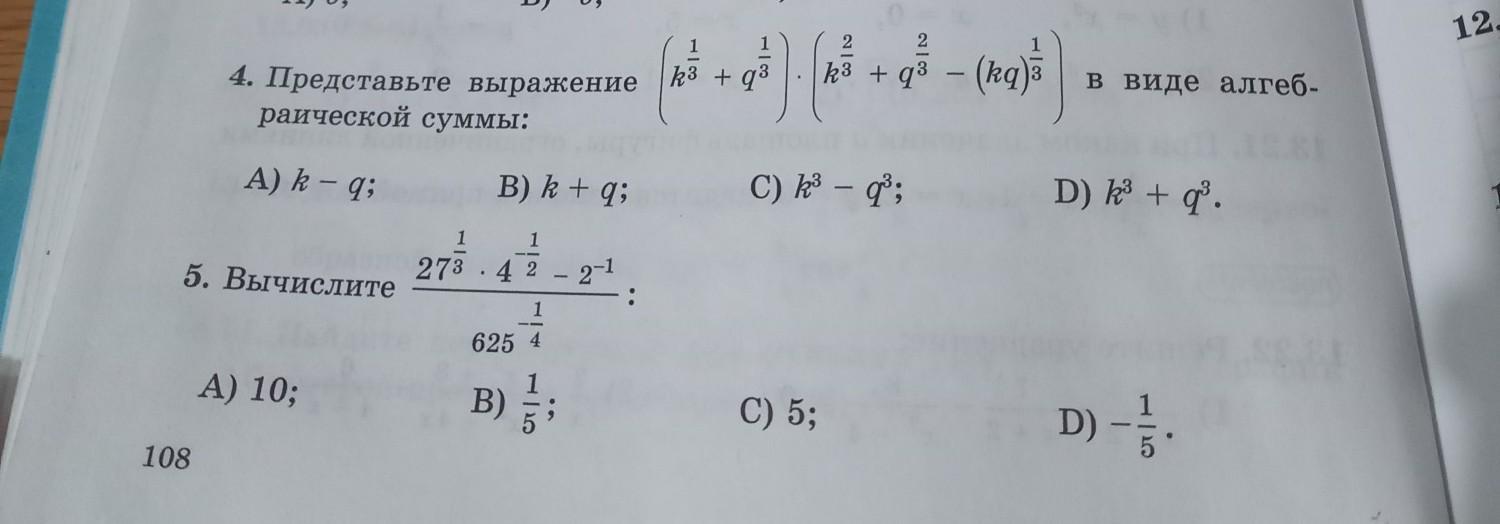
Ответы
Автор ответа:
1
Ответ:
Автор ответа:
1
Похожие вопросы
Предмет: Английский язык,
автор: анька88
Предмет: Английский язык,
автор: Кира27546884699
Предмет: Русский язык,
автор: dimazemlyakov
Предмет: История,
автор: fjJsjshwjks
Предмет: Математика,
автор: any1523