Предмет: Алгебра,
автор: Аноним
Помогите решить задачи пожалуйста
Приложения:
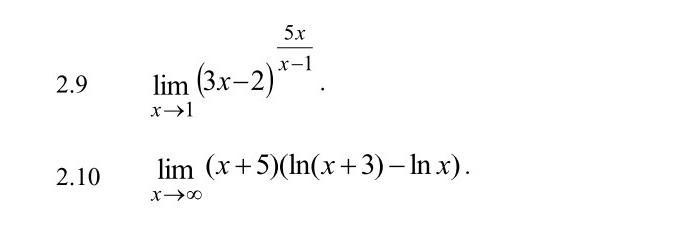
Ответы
Автор ответа:
1
Ответ:
Объяснение:
!!!!!!!!!!!!!!!!!!!!!!!!!!
Приложения:

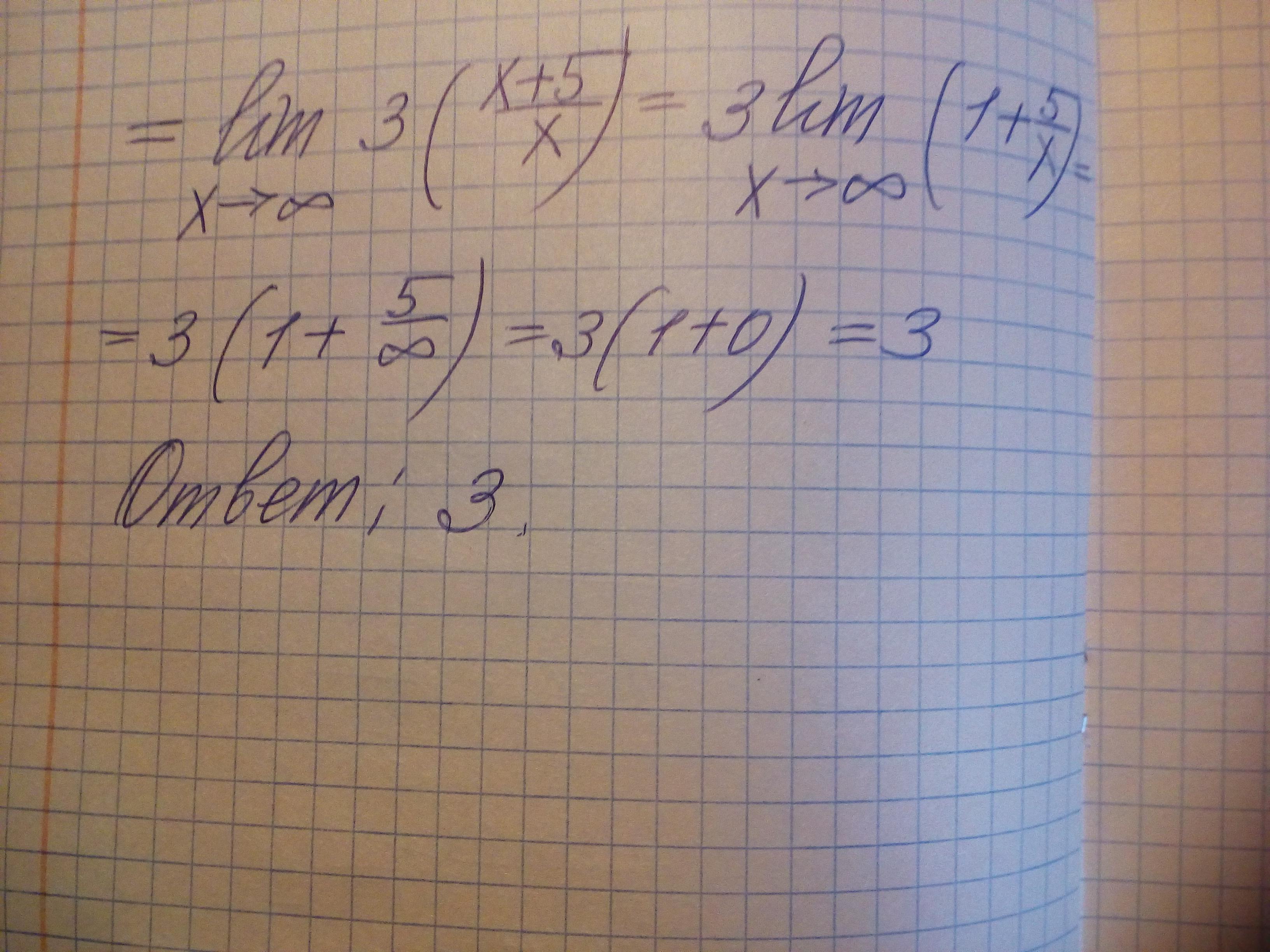
Автор ответа:
1
Объяснение:
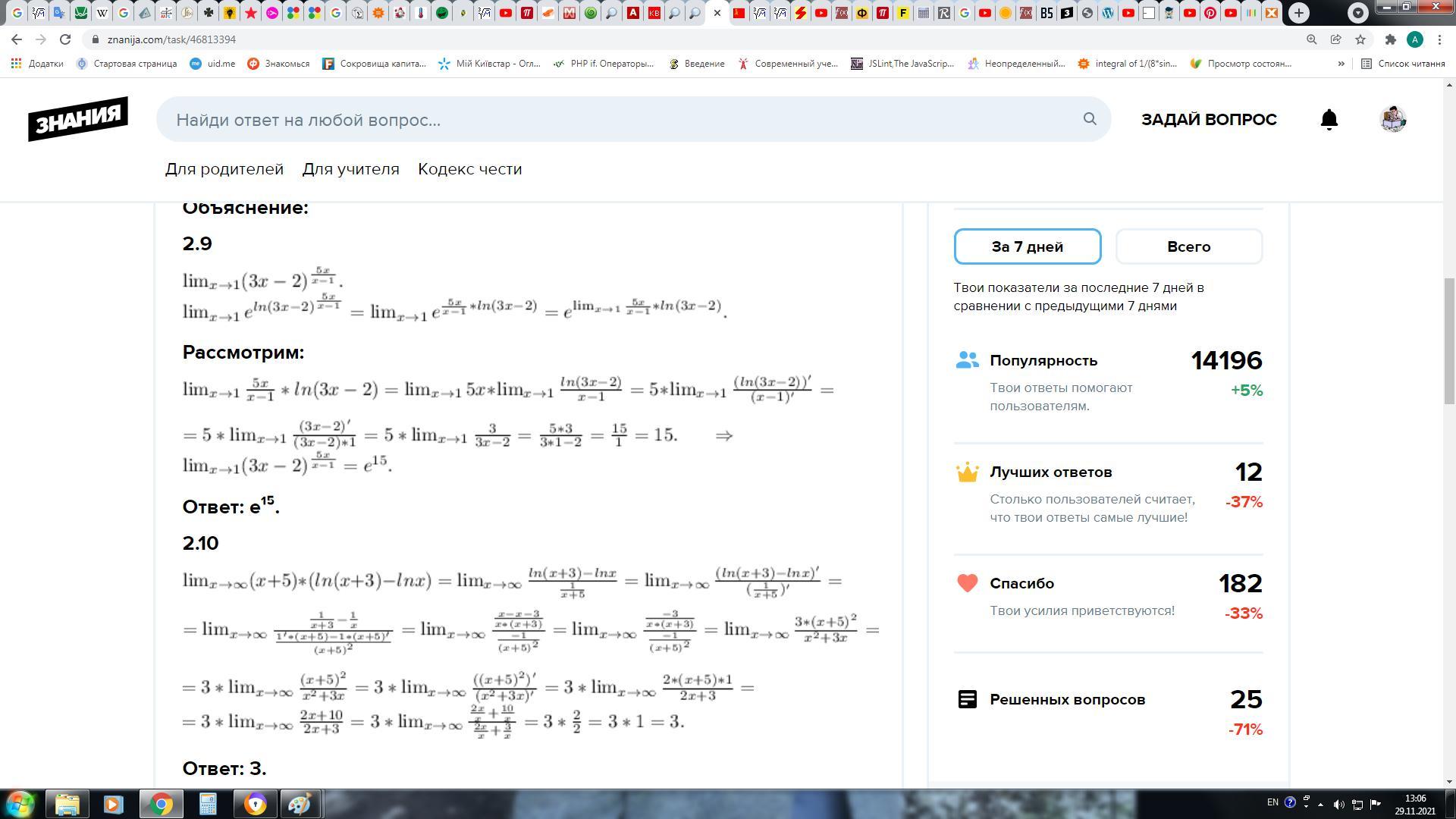
2.9
Рассмотрим:
Ответ: e¹⁵.
2.10
Ответ: 3.
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: ХорошисткаEli
Предмет: Английский язык,
автор: vladikchireev
Предмет: Русский язык,
автор: ЗвезднаяДевочка
Предмет: Литература,
автор: scorpion3665
Предмет: Английский язык,
автор: Katya73737