Предмет: Алгебра,
автор: wrx102018
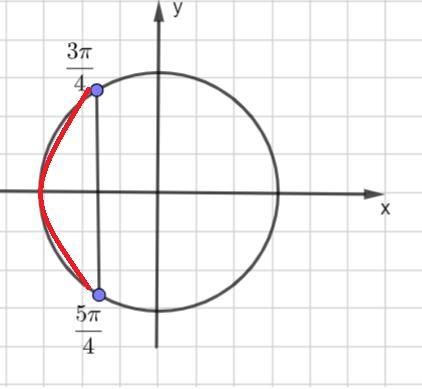
найдите решение неравенства 1/2cos3x+√3/2sin3x<-√2/2
Ответы
Автор ответа:
2
Ответ:
Объяснение:
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: егор486
Предмет: Русский язык,
автор: 3in184
Предмет: Українська мова,
автор: Polishchuk11
Предмет: Русский язык,
автор: semjaschilowi
Предмет: Литература,
автор: yablochkin2004