Предмет: Алгебра,
автор: istepanov500
Уравнения. 90 баллов.
Приложения:
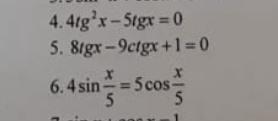
Ответы
Автор ответа:
0
Ответ:
Похожие вопросы
Предмет: Русский язык,
автор: irinaSD85
Предмет: Английский язык,
автор: zemoga15
Предмет: Українська література,
автор: Аноним
Предмет: Английский язык,
автор: fha231
Предмет: Алгебра,
автор: asynagortinskay