Предмет: Алгебра,
автор: istepanov500
Помогите решить уравнения, дам 100 баллов.
Приложения:
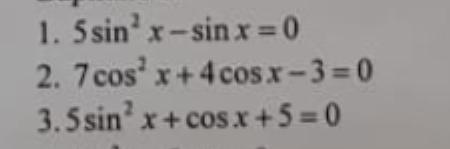
Ответы
Автор ответа:
0
Ответ:
Похожие вопросы
Предмет: Русский язык,
автор: Софи20062016
Предмет: Окружающий мир,
автор: layiq3
Предмет: Другие предметы,
автор: мила305
Предмет: Химия,
автор: vakulenko101
Предмет: Математика,
автор: Аноним