Предмет: Алгебра,
автор: Kotyt189
Помогите решить, дам 30 баллов
Приложения:

Ответы
Автор ответа:
1
Ответ:прикрепила
Найдите значение выражения 6^15×6^-13=6^2=36
Представьте выражение в виде рацональной дроби
Объяснение:
Приложения:
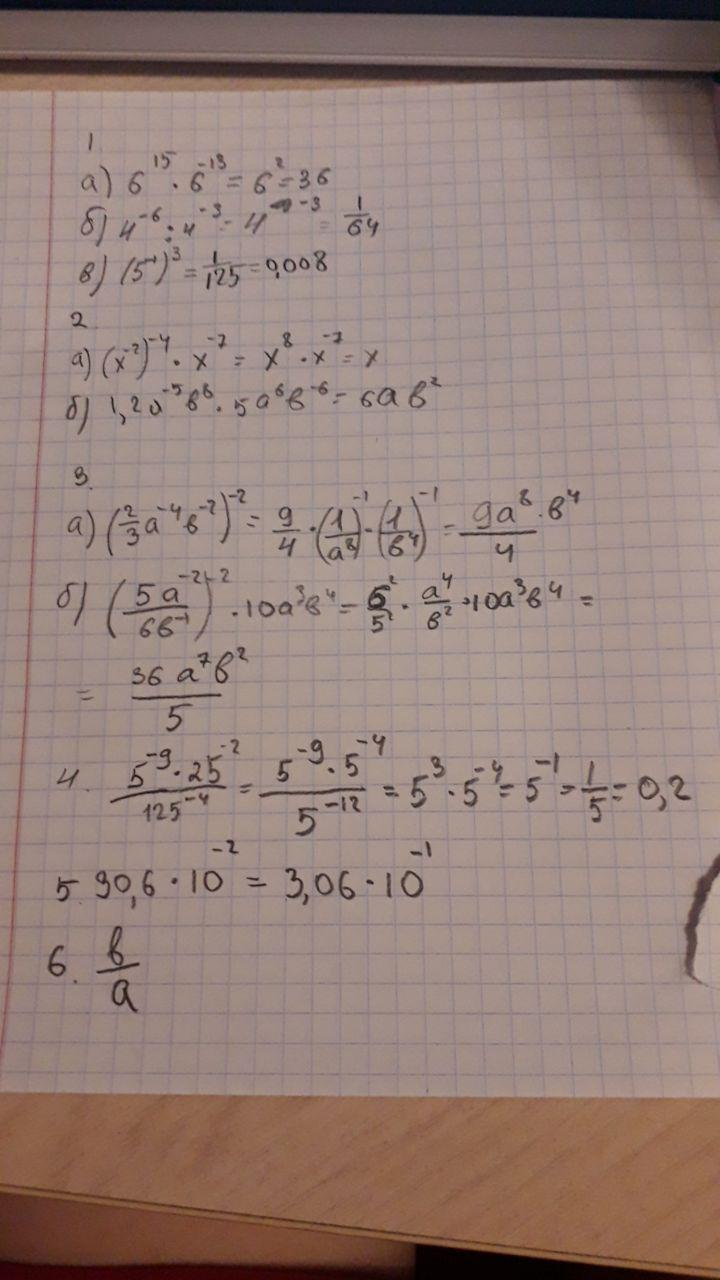
Автор ответа:
1
Объяснение:
1.
а)
б)
в)
2.
а)
б)
3.
а)
б)
4.
5.
6.
Похожие вопросы
Предмет: Окружающий мир,
автор: nurislamkamalet
Предмет: Русский язык,
автор: Ринат2281
Предмет: Русский язык,
автор: svetkos1
Предмет: Математика,
автор: Xymka
Предмет: Математика,
автор: Haskov1104