помогите, пожалуйста
Даны: точка А, уравнения прямой и плоскости. Найти: а) угол между прямой и плоскостью, Б)уравнение прямой, проходящей через точку А перпендикулярно данной плоскости; в) уравнение плоскости, проходящей через точку А перпендикулярно прямой; г) расстояние от точки до прямой; д) расстояние от точки до плоскости.
УСЛОВИЕ НА ФОТО
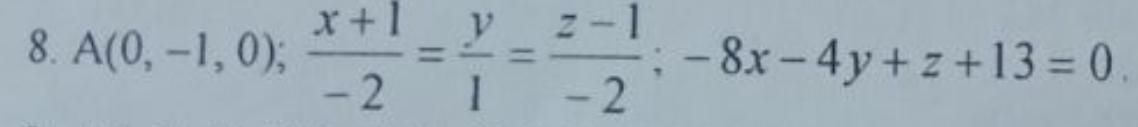
Ответы
Даны: точка А(0; -1; 0), уравнения прямой (x + 1)/(-2) = y/1 = (z – 1)/(-2) и плоскости -8x – 4y + z + 13 = 0.
Найти:
а) угол между прямой и плоскостью.
Направляющий вектор прямой имеет вид:
n1 = {-2; 1; -2}.
Вектор нормали плоскости имеет вид:
n = {-8; -4; 1}.
Угол между прямой и плоскостью:
sinφ = | -2 · (-8) + 1 · (-4) + (-2) · 1 |
√((-2)2 + 12 + (-2)2) · √((-8)2 + (-4)2 + 12) =
= (16-4-2)/(√9*√81) = 10/(3*9)=10/27.
Угол равен arcsin(10/27) = 21,73846 градуса.
б) уравнение прямой, проходящей через точку А перпендикулярно данной плоскости.
Для этой прямой (пусть это будет АК) вектор нормали плоскости n = {-8; -4; 1} будет направляющим вектором.
Получаем уравнение:
АК: x/(-8) = (y + 1)/(-4) = z/1.
в) уравнение плоскости, проходящей через точку А перпендикулярно прямой.
Для этой плоскости направляющий вектор прямой n1 = {-2; 1; -2} будет нормальным вектором.
Подставим его координаты в уравнение плоскости с учётом точки (-1; 0; 1), принадлежащей плоскости.
-2(x + 1) + 1*y – 2*(z – 1) = 0,
Получаем уравнение 2x – y + 2z = 0.
г) расстояние от точки до прямой.
Из уравнения прямой получим:
s = -2; 1; -2 - направляющий вектор прямой;
M1 = -1; 0; 1 - точка, лежащая на прямой.
Тогда
M0M1 = {M1x - M0x; M1y - M0y; M1z - M0z} = (-1 - 0; 0 - (-1); 1 – 0( = (-1; 1; 1).
Площадь параллелограмма лежащего на двух векторах M0M1 и s:
S = |M0M1 × s|
M0M1 × s = i j k
-1 1 1
-2 1 -2 =
= i (1·(-2) - 1·1) - j (-1·(-2) - 1·(-2)) + k (-1·1 - 1·(-2)) =
= i (-2 – 1) - j (2 + 2) + k( -1 + 2) =
= (-3; -4; 1).
Зная площадь параллелограмма и длину стороны найдем высоту (расстояние от точки до прямой):
d = |M0M1×s|/|s| = √(-3)2 + (-4)2 + 12/√(-2)2 + 12 + (-2)2 = √26/√9 = √26/3 ≈ 1,69967.
д) расстояние от точки А(0; -1; 0) до плоскости -8x – 4y + z + 13 = 0.
Для вычисления расстояния от точки M(Mx; My; Mz) до плоскости Ax + By + Cz + D = 0.
используем формулу:d = |A·Mx + B·My + C·Mz + D|/√(A² + B² + C²).
Подставим в формулу данные:
d = |-8·0 + (-4)·(-1) + 1·0 + 13|/√((-8)² + (-4)² + 1²) = |0 + 4 - 0 + 13|/√(64 + 16 + 1) = 17/√81 = 17/9 ≈ 1,88889.