Предмет: Геометрия,
автор: irinapawlenko4
Пожалуйста помогите решить, даю 100 балов
Приложения:

Ответы
Автор ответа:
0
Ответ:
Объяснение:
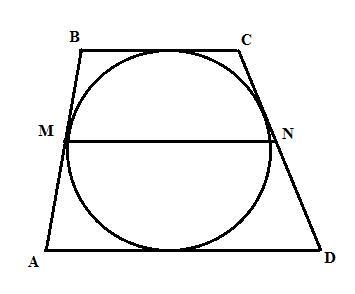
Пусть ABCD - трапеция, описанная около окружности, MN - средняя линия. В четырехугольник можно вписать окружность тогда и только тогда, когда суммы длин его противолежащих сторон равны. Также и для трапеции AB+CD=BC+AD. При этом средняя линия трапеции MN=(BC+AD)/2
P(ABCD)=AB+CD+BC+AD=2*(BC+AD)
P(ABCD)/MN=2*(BC+AD) / (BC+AD)/2 = 4
Что и требовалось доказать - периметр описанной трапеции в 4 раза больше её средней линии.
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: danchik38
Предмет: Русский язык,
автор: 123456789699
Предмет: Русский язык,
автор: ghjcnj87
Предмет: Математика,
автор: cecenovalarisa
Предмет: Алгебра,
автор: kanetta