Предмет: Математика,
автор: denissro
ПОМОГИТЕ РЕШИТЬ ПОКАЗАТЕЛЬНОЕ УРАВНЕНИЕ!!С РЕШЕНИЕМ
Приложения:
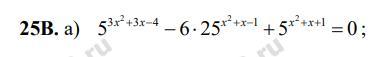
Ответы
Автор ответа:
0
, поэтому делим обе части уравнения.
Берём замену . Тогда:
.
Обратная замена.
Решим уравнения отдельно.
1)
2)
Итого имеем 4 корня:
Ответ:
Похожие вопросы
Предмет: Английский язык,
автор: mtn2010
Предмет: Русский язык,
автор: ДимаТюрин
Предмет: Английский язык,
автор: Аноним
Предмет: Химия,
автор: zaharnuchev7331
Предмет: Математика,
автор: bogdankripak228