Предмет: Математика,
автор: denissro
ПОМОГИТЕ РЕШИТЬ ПОКАЗАТЕЛЬНОЕ УРАВНЕНИЕ!!С РЕШЕНИЕМ
Приложения:
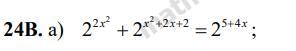
Ответы
Автор ответа:
0
Так как , то смело делим обе части уравнения.
Возьмём замену , при этом
. Тогда:
.
Второй корень не удовлетворяет области определения замены (), значит, рассматриваем только первый.
Уравнение имеет два корня.
Ответ: .
Похожие вопросы
Предмет: Английский язык,
автор: yakalinohka1
Предмет: Русский язык,
автор: bosss2001
Предмет: Английский язык,
автор: Аноним
Предмет: Информатика,
автор: 4EREP1
Предмет: Қазақ тiлi,
автор: moni5176