Предмет: Геометрия,
автор: Petrograf
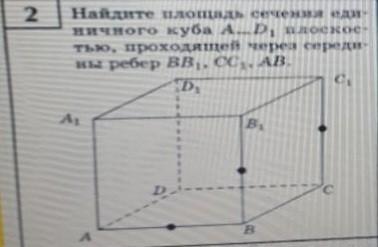
Найдите площадь сечения единичного куба A...D1 плоскомтью,проходящей через середины рёбер BB1,CC1,AB
Приложения:
Ответы
Автор ответа:
4
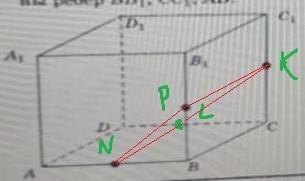
Чтобы построить сечение, проведем на нижней грани куба (см. рисунок) прямую NP║ВС, где N - середина АВ, P - середина DC. Затем соединим между собой точки N, L, K, P. В сечении получится прямоугольник NLKP.
Его площадь равна: S = NL * LK = 0,5 * AB₁ * BC = 0,5 * √2 * 1 = .
AB₁ - диагональ квадрата, которая вычисляется как гипотенуза в равнобедренном прямоугольном треугольнике с катетами, равными единице. NL - средняя линия треугольника AB₁В.
Ответ: площадь сечения равна квадратных единиц.
PS. На нормальном чертеже отрезки NP и KP нужно изображать пунктирными линиями, ибо они скрыты от наблюдателя снаружи куба.
Приложения:
Petrograf:
можешь ещё ответить ?
Похожие вопросы
Предмет: Окружающий мир,
автор: Аноним
Предмет: Другие предметы,
автор: Киса5588
Предмет: Русский язык,
автор: ЛовецМандаринов
Предмет: Беларуская мова,
автор: sofyco