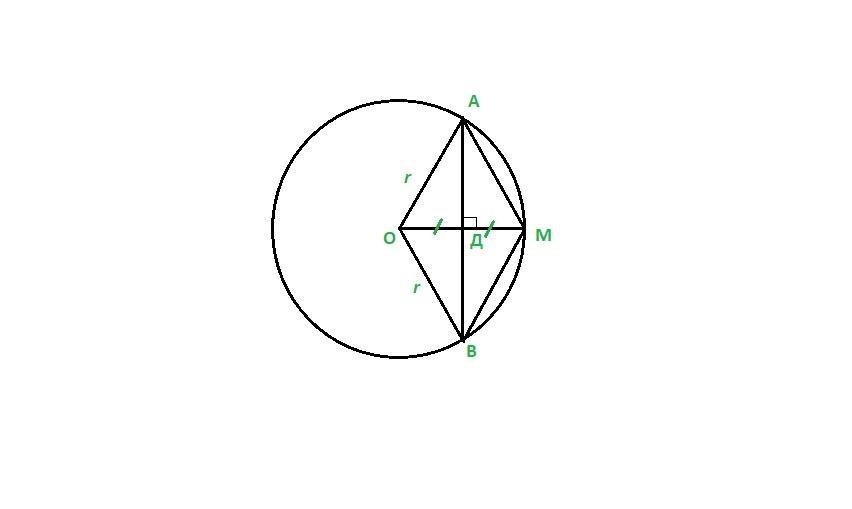
Точка O - центр окружности. Хорда AB перпендикулярна радиусу OM и делят его пополам. Найдите углы AOB и BAM.
Ответы
Ответ:
120°; 30°
Объяснение:
Дано: Окр.О,OM.
AB - хорда;
МН = НО.
Найти: ∠AOB и ∠BAM.
Решение:
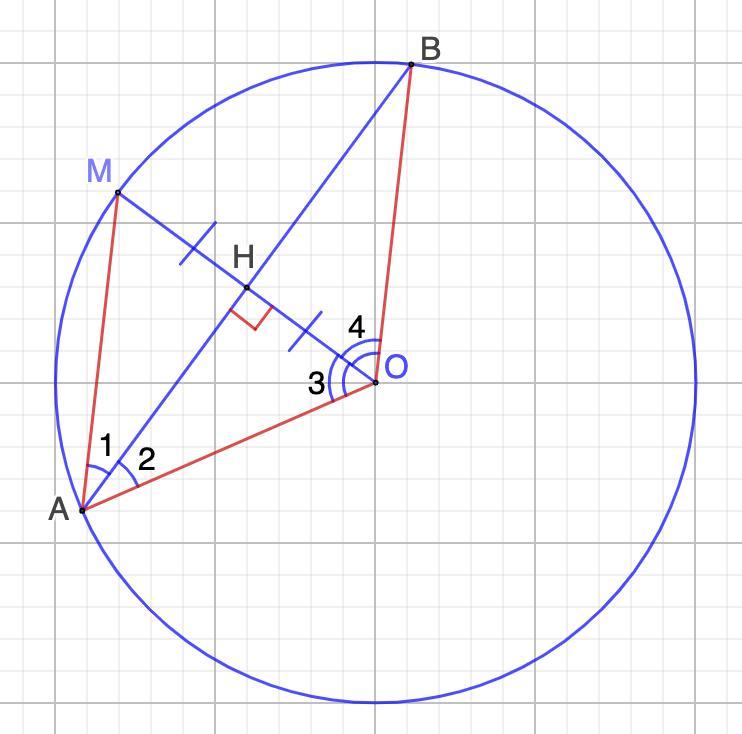
1) Рассмотрим ΔАМО.
АН ⊥ МО (условие) ⇒ АМ - высота.
МН = НО (условие) ⇒ АМ - медиана.
- Если в треугольнике высота является медианой, то треугольник - равнобедренный.
⇒ ΔАМО - равнобедренный.
⇒ АО = АМ = R.
АО = ОМ = R
⇒ ΔАМО - равносторонний.
- В равностороннем треугольнике углы равны.
⇒ ∠А = ∠М = ∠3 = 180° : 3 = 60°
- В равнобедренном треугольнике высота , проведенная к основанию, является медианой и биссектрисой.
⇒ ∠1 = ∠2 = 60° :2 = 30°
∠ВАМ = 30°
2. Рассмотрим ΔАВО.
АО = ОВ = R
⇒ ΔАВО - равнобедренный.
ОН - высота (условие)
⇒ ОН - биссектриса.
∠3 = ∠4 = 60°
⇒ ∠АОВ = 120°
Ответ:
∠AOB=120° ∠BAM=30°
Объяснение:
ΔАОД=ΔАМД по двум катетам (АД- общий, ОД=ДМ - по условию)
⇒АО=АМ= r
Аналогично из равенства треугольников ВОД и ВМД : ОВ=ВМ= r
Таким образом все стороны четырёхугольник АМВО равны между собой и равны r.
ΔАДМ=ΔВДО - по катету и гипотенузе (ОД=ДМ - по условию, АМ=ОВ=r)
Из равенства треугольников следует равенство сторон: АД=ВД.
Если диагонали четырёхугольника пересекаются и точкой пересечения делятся пополам, то такой четырёхугольник является параллелограммом.
⇒АМВО - параллелограмм. А параллелограмм у которого все стороны равны является ромбом.
Прямоугольный ΔАДО: Катет ОД = 1/2 * ОМ = 1/2* r
Гипотенуза ОА = r
Катет, равный половине гипотенузы, лежит против угла 30 градусов. ⇒∠ОАД=∠ВАМ= 30°
∠ОАМ = 2* ∠ОАД = 2*30°=60°
∠ОАМ и ∠AOB - внутренние односторонние углы при параллельных прямых АМ и ОВ и секущей АО. Их сумма равна 180°
⇒∠AOB=180°-∠ОАМ = 180°-60°=120°