Question

3. ABCD выпуклый четырёхугольник, где АВ = 7, BC = 4, AD = DC, угол ABD = углу DBC. Точка E на отрезке АВ такова, что ZDEB = 90°. Найдите
длину отрезка АЕ.

Answer 1

Ответ:

1,5 ед.

Пошаговое объяснение:

Дано: ABCD - выпуклый четырёхугольник.

АВ = 7, BC = 4,

AD = DC,

∠ ABD = ∠ DBC,

∠DEB = 90°.

Найти: АЕ

Решение:

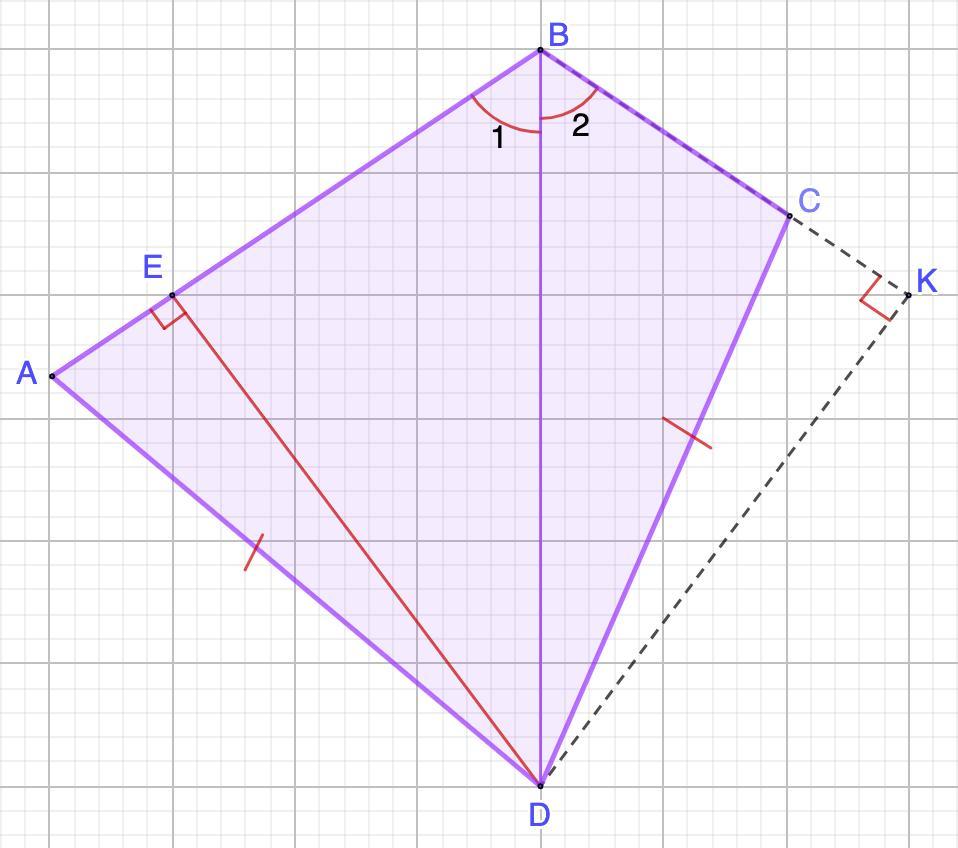
Проведем DK ⊥ BC.

1. Рассмотрим ΔЕВD и ΔDBK - прямоугольные.

∠1 = ∠2 (по условию)

BD - общая.

⇒ ΔЕВD = ΔDBK (по гипотенузе и острому углу)

• В равных треугольниках против равных углов лежат равные стороны.

⇒ ED = DK;  EB = BK.

2. Рассмотрим  ΔАЕD и ΔВСК - прямоугольные.

ED = DK (п.1)

AD = DC (по условию)

⇒ ΔАЕD = ΔВСК (по гипотенузе и катету)

⇒ АЕ = СК

3.  Пусть АЕ = СК = х

ЕВ = АВ - АЕ = 7 - х

ВК = ВС + х = 4 + х

ЕВ = ВК (п.1)

⇒ 7 - х = 4 + х

    2х = 3

     х = 1,5

⇒ АЕ = 1,5