Question

Прямая l, проходящая через середину стороны АС треугольника АВС, пересекает стороны ВА и ВС угла АВС в точках D и E соответственно. Докажите, что если BD = BE, то AD = CE.

Answer 1

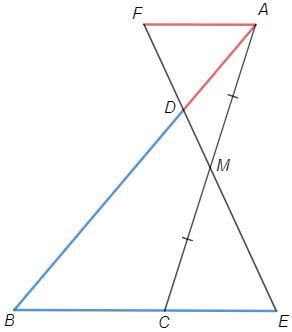
Через точку A проведем параллельную BC, прямая DE пересекает ее в точке F.

∠FAC=∠ECA (накрест лежащие при AF||BС)

∠AMF=∠CME (вертикальные)

△AMF=△CME (по стороне и прилежащим углам)

=> AF=CE

△BDE~△ADF (по накрест лежащим при AF||BС)

△BDE - р/б (BD=BE) => △ADF -р/б, AF=AD

=> AD=AF=CE

Или по т Менелая (BD/BE=1, AM/MC=1)

BD/DA *AM/MC *CE/EB =1 => BD/EB *CE/DA =1 => CE/DA =1