Предмет: Алгебра,
автор: llingovsky
Доведіть тотожність срочно надо
Приложения:
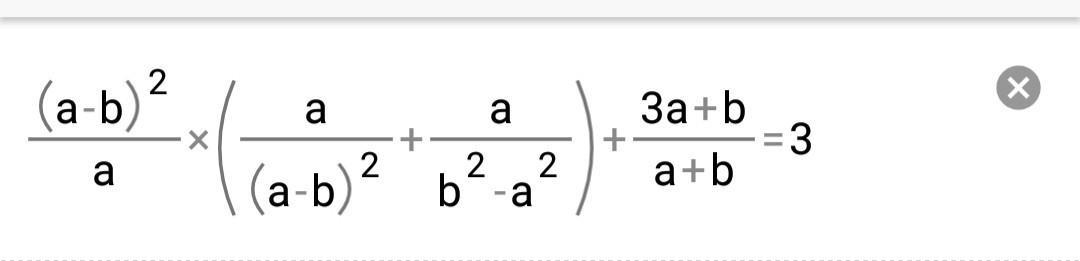
Ответы
Автор ответа:
1
Ответ:
Объяснение:
Похожие вопросы
Предмет: Окружающий мир,
автор: golovko1962
Предмет: Русский язык,
автор: Тимофей200611
Предмет: Другие предметы,
автор: vipasema2009mailru
Предмет: Алгебра,
автор: Аноним
Предмет: Русский язык,
автор: fatimaevlo1971