Question

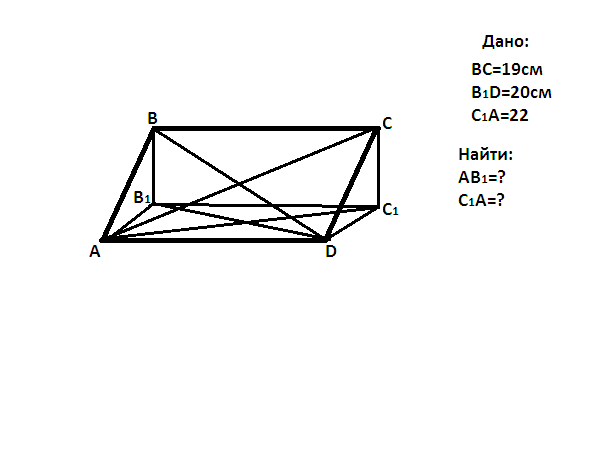
Плоскость а проведена через сторону AD параллелограмма ABCD.Найдите проекции сторон параллелограмма на эту плоскость, если BC=19 и проекции диагоналей параллелограмма на плоскость а равны 20 и 22.  Рисунок вроде правильный

Answer 1

Плоскость а проведена через сторону AD параллелограмма ABCD.Найдите проекции сторон параллелограмма на эту плоскость, если BC=19 и проекции диагоналей параллелограмма на плоскость а равны 20 и 22.  

АС1 находить нет нужды, она по условию равна 22. 
Рассмотрим данный к задаче рисунок. и проекции АВ1 и В1С1 сторон АВ и ВС параллелограмма ABCD  на плоскость α.
Так как ВС параллельна прямой АD, лежащей на плоскости α, она параллельна и самой плоскости α.
 Поэтому проекция В1С1 стороны ВС на плоскость равна 19. 
Проекции диагоналей на плокость равны диагоналям параллелограмма АВ1С1D со сторонами АД=В1С1=19. 
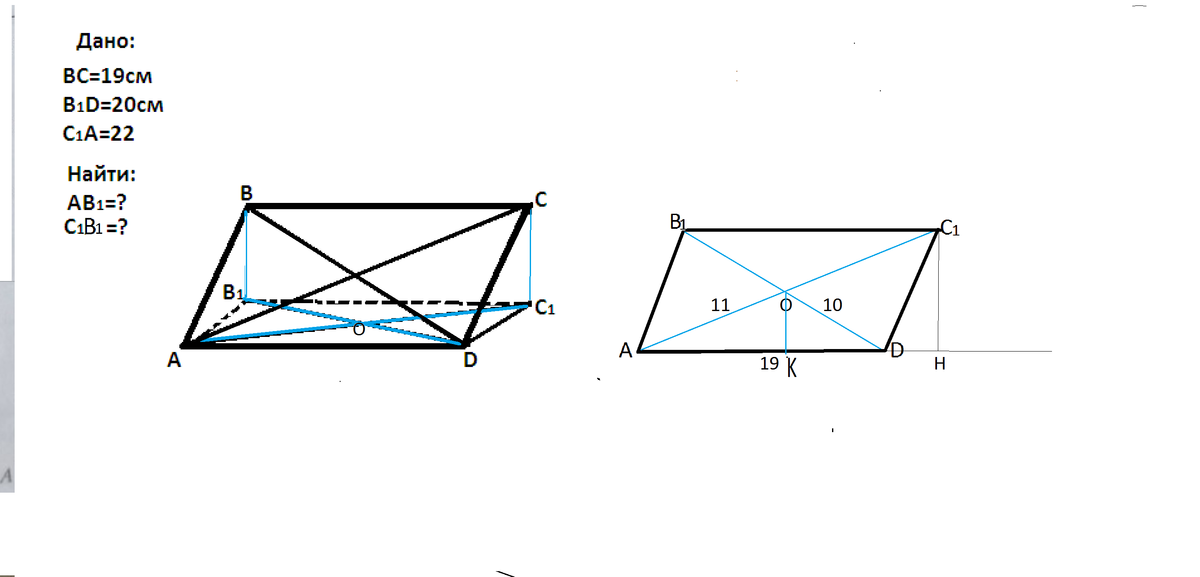
Нарисуем этот параллелограмм AB1C1D. 
По формуле Герона найдем площадь треугольника АОD
 Полупериметр треугольника АОД=(11+10+19):2=20 
S=√1800=30√2 
Из площади треугольника АОД найдем его высоту ОК к основанию АД по формуле площади  треугольника:
S=аh:2
2S= 60√2 
ОК=60√2:19=4,4659.....≈ 4,466 
Продлим АД до пересечения с высотой С1Н, опущенной из С1, 
и получим прямоугольный треугольник АС1Н. 
С1Н=2ОК= ≈ 8,93 
Найдем в нем сторону АН по т. Пифагора. 
АН=√(АС1²-НС1²)≈ √(22²-8,93²)=√(484-79,7449)=≈20,1 
Отсюда ДН=20,1-19=1,1 
Из треугольника ДНС1 найдем длину ДС1, она равна также и АВ1.
ДС1=√(НС1²+НД²)=√(79,7449+1,21)=√80,9549=8,9974≈9