Question

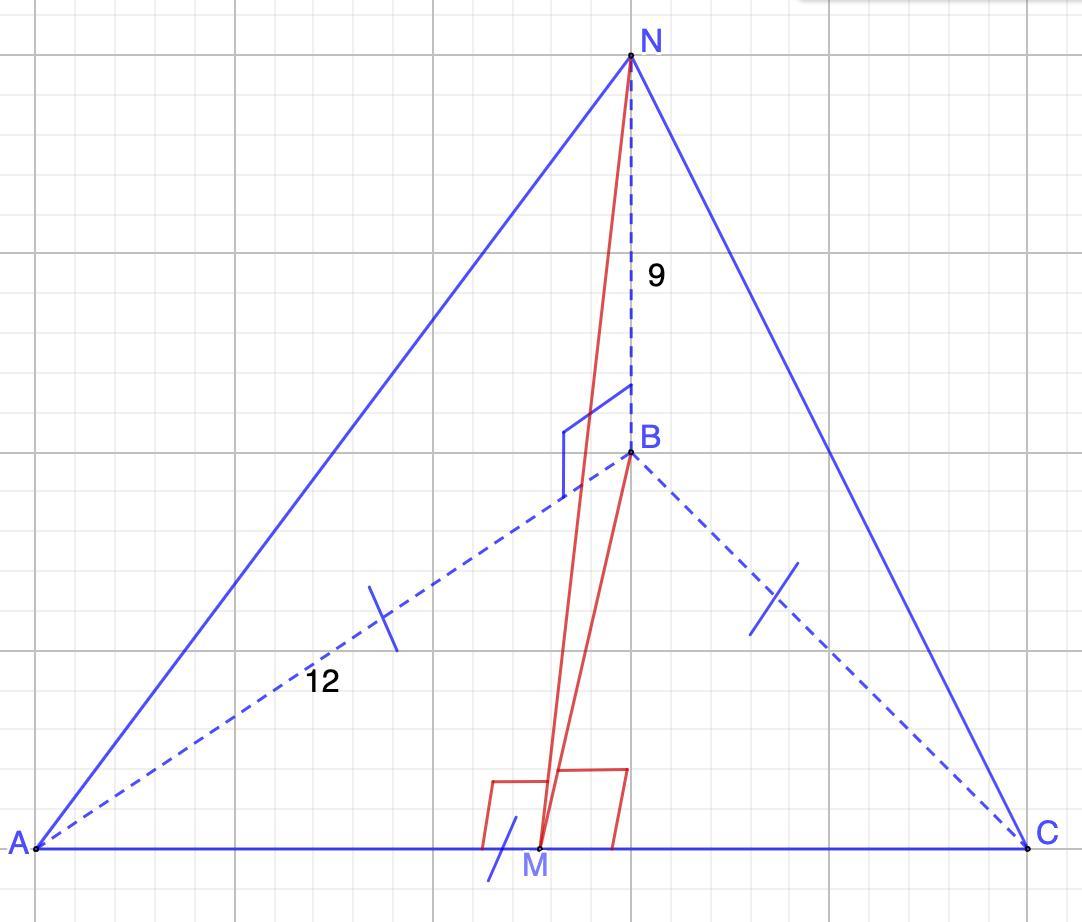
Задан равносторонний треугольник ABC со стороной AB = 12. Отрезок BN, равный 9, перпендикулярен плоскости треугольника ABC. Найдите площадь треугольника ANC.

В ЗАДАНИИ НЕОБХОДИМО ВЫПОЛНИТЬ РИСУНОК

Answer 1

Ответ:

18√21 cм²

Объяснение:

ΔABC - равносторонний ⇒ ∠А=∠В=∠С=60°; АВ=ВС=АС=12см

В ΔABC проведём высоту ВD⊥АС. Т.к. ΔABC - равносторонний, то ВD является также биссектрисой и медианой.

АD=DС=12/2=6 см

BN перпендикулярен плоскости треугольника ABC ⇒

BN перпендикулярен любой прямой в этой плоскости ⇒

BN⊥ВD.

BN⊥ВD,  ВD⊥АС ⇒ по "теореме о трёх перпендикулярах" ND⊥АС.

Рассмотрим прямоугольный ΔDBC(∠D=90°). По т.Пифагора найдём катет ВD:

ВD²=ВС²-DС²=12²-6²=144-36=108

Рассмотрим прямоугольный ΔNBD(∠B=90°). По т.Пифагора найдём гипотенузу :

ND²=NB²+ВD²=9²+108=81+108= 189

ND =$\sqrt{189} =\sqrt{9*21} =3\sqrt{21}$ см

SΔANC = $\frac{1}{2} *AC*ND= \frac{1}{2} *12 * 3\sqrt{21} = 18\sqrt{21}$  cм²

Answer 2

Ответ:

18√21 ед².

Объяснение:

Дано: ΔАВС - равносторонний.

АВ = 12; BN = 9

BN ⊥ ABC

Найти: S (ΔANC)

Решение:

Проведем высоту NM в ΔANC.

NM ⊥ AC

• Обратная теорема: прямая, проведенная в плоскости через основание наклонной перпендикулярно к ней, перпендикулярна и к ее проекции.

⇒ ВМ ⊥ АС.

1. Рассмотрим ΔАВС - равносторонний.

ВМ - высота.

• В равнобедренном треугольнике высота , проведенная к основанию,  является медианой.

⇒ АМ = МС = 12 : 2 = 6 (см)

2. Рассмотрим ΔАВМ - прямоугольный.

По теореме Пифагора:

$BM^2=BC^2-MC^2=144-36 = 108\\\\BM=\sqrt{108}=6\sqrt{3}$

3. Рассмотрим ΔMNB - прямоугольный.

По теореме Пифагора:

$MN^2=MB^2+NB^2 = 108+81 = 189\\\\MN=3\sqrt{21}$

4. Найдем площадь ΔANC.

• Площадь треугольника равна половине произведения основания на высоту.

$\displaystyle S_{ANC}=\frac{1}{2}*AC*MN=\frac{1}{2}*12* 3\sqrt{21}=18\sqrt{21}$