Предмет: Алгебра,
автор: xxx1Ren
Помогите, пожалуйста, решить данное неравенство.
Фото задания прикрепляется
Приложения:
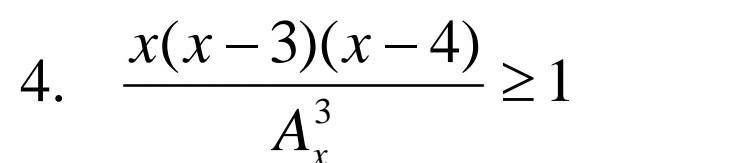
Ответы
Автор ответа:
1
+ + + + + (0) - - - - - (1) + + + + + (2) - - - - - [2,5] + + + + +
//////////// ///////////
Похожие вопросы
Предмет: Немецкий язык,
автор: никита1632
Предмет: Русский язык,
автор: Åľıśâ
Предмет: Английский язык,
автор: рома651
Предмет: Математика,
автор: Аноним
Предмет: Математика,
автор: voznas