Предмет: Алгебра,
автор: ksenyadanilova04
Помогите пожалуйста с алгеброй 8 класс
Приложения:
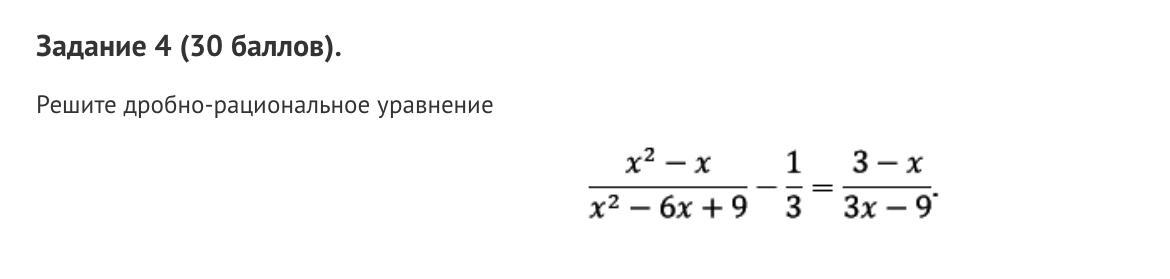
Ответы
Автор ответа:
2
Ответ:
*
По т. Виета
Похожие вопросы
Предмет: Беларуская мова,
автор: witherman8
Предмет: Окружающий мир,
автор: argoko
Предмет: Русский язык,
автор: Na2008
Предмет: Английский язык,
автор: Викуся1234о
Предмет: Математика,
автор: Максим228822