Предмет: Алгебра,
автор: nastelka05
Докажите, что функция является чётной
Приложения:
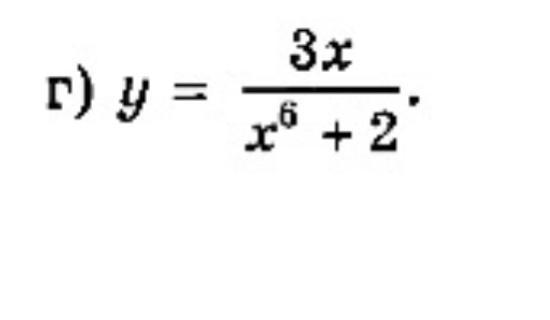
Ответы
Автор ответа:
0
y = 3x/(x⁶ + 2)
• Найдём область определения:
D (y) : x⁶ + 2 ≠ 0
x⁶ ≠ -2
x⁶ ≥ 0 при любых значениях «x», ⇒
D (y) = ℝ
Доказать, что y (x) - чётная функция
Доказательство:
• Функция является чётной, тогда и только тогда, когда:
y (-x) = y (x)
А нечётной, если:
y (-x) = -y (x)
• Проверяем:
y(-x) = (3 • (-x))/((-x)⁶ + 2) = -3x/(x⁶ + 2) = -(3x/(x⁶ + 2)
• Получается y (-x) = -y (x), ⇒ функция является НЕЧЁТНОЙ, а не чётной
nastelka05:
А какая область определения?
x⁶ + 2 ≠ 0, ⇒ x⁶ = -2, а x⁶ ≥ 0, ⇒ D (y) = ℝ
Похожие вопросы
Предмет: Русский язык,
автор: Сафинур
Предмет: Русский язык,
автор: Natali212223
Предмет: Окружающий мир,
автор: макоровсергей2005
Предмет: История,
автор: 50050014
Предмет: Математика,
автор: arina200828