Предмет: Геометрия,
автор: jhsahjlffssfdj
35 баллов
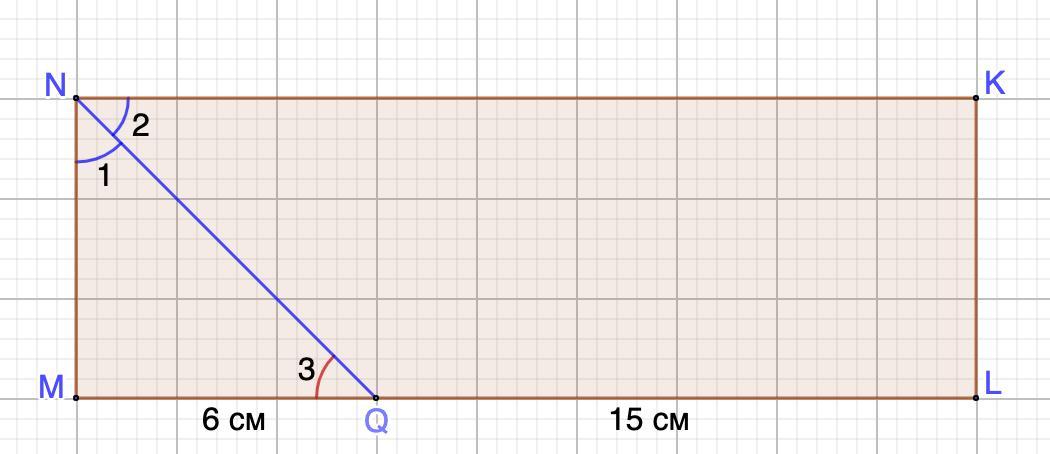
Дан прямоугольник MNKL . Биссектриса угла N пересекает сторону ML в точке Q . MQ=6 см и QL=15 см. Найди площадь прямоугольника MNKL .
Ответы
Автор ответа:
1
Ответ:
126 см²
Объяснение:
Дано: MNKL - прямоугольник.
NQ - биссектриса.
MQ=6 см; QL=15 см.
Найти: S (MNKL)
Решение:
1. Рассмотрим ΔMNQ.
∠1 = ∠2 (NQ - биссектриса)
∠3 = ∠2 (накрест лежащие при ML || NK т секущей NQ)
⇒ ∠1 = ∠3
- Если у треугольника два угла равны, то этот треугольник — равнобедренный.
⇒ ΔMNQ - равнобедренный
⇒ MQ = MN = 6 см
2. Рассмотрим MNKL - прямоугольник
- Площадь прямоугольника равно произведению смежных сторон.
Приложения:
shiftstfu:
правильно?
Не знаю
Похожие вопросы
Предмет: Английский язык,
автор: dezz114
Предмет: Русский язык,
автор: Vesna04
Предмет: Русский язык,
автор: Dina3232
Предмет: Математика,
автор: marina223425
Предмет: Русский язык,
автор: nastia7539