Предмет: Математика,
автор: Аноним
Помогите решить это даю за это 50 баллов
Приложения:

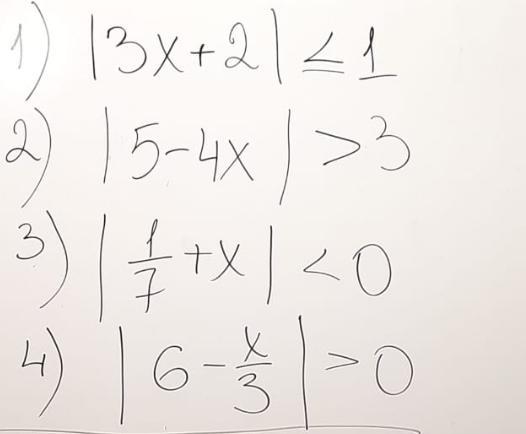
Ответы
Автор ответа:
1
Пошаговое объяснение:
- Вспомним: Если обе части неравенства умножить или разделить на отрицательное число, знак неравенства перевернется.
Данное неравенство равносильно системе:
Это неравенство равносильно совокупности:
Данное неравенство решений не имеет, так как модуль числа неотрицателен.
Это неравенство справедливо при любом значении х, кроме значения х, при котором подмодульное выражение равно 0. Найдем это значение:
Это неравенство равносильно системе:
Похожие вопросы
Предмет: Английский язык,
автор: SophiaKolesova
Предмет: Русский язык,
автор: shatroff17
Предмет: Русский язык,
автор: zozulyanuriya
Предмет: Алгебра,
автор: fashilinav
Предмет: Алгебра,
автор: kristinapolunicheva2