Question

Площадь параллелограмма МNKL равна 368 м квадратных. Точка Q - середина стороны LK. Найди площадь треугольника MLQ.

Answer 1

Ответ:

92 м²

Объяснение:

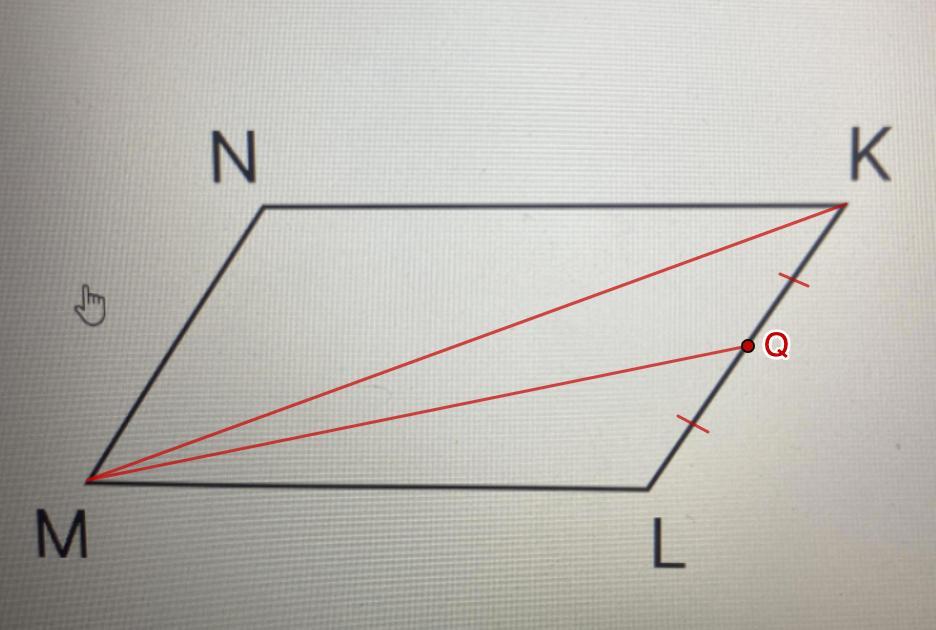
Дано: MNKL - параллелограмм.

LQ = QK

S (MNKL) = 368 м²

Найти: S (ΔMLQ)

Решение:

МК - диагональ.

• Диагональ параллелограмма делит его на два равных треугольника.

⇒ S (ΔMNK) = S (ΔMKL) = S (MNKL) : 2 = 368 :2 = 184 (м²)

Рассмотрим ΔMKL.

LQ = QK (условие)

⇒ MQ - медиана.

• Медиана делит треугольник на два равновеликих треугольника.

⇒ S (ΔMLQ) = S (ΔMKL) : 2 = 184 : 2 = 92 (м²)

Answer 2

Ответ:

92 кв.см

Объяснение:

Площадь параллелограмма равна половине произведения диагоналей на синус угла между ними: S=ML×LK×sin(L)=368

Площадь треугольника: S= 0,5×ML×LQ×sin(L) т.к Q-середина LK, то LQ=0.5×LK, тогда формула площади треугольника примет вид:

S= 0,5×ML×0.5×LK×sin(L)= 0.25×ML×LK×sin(L),

но ML×LK×sin(L)=368, =>

S треугольника = 0.25× S паралелограма = 0.25×368=92 кв.см