Небольшой грузик массой m подвешен на легкой нерастяжимой нити длиной l. При малом отклонении грузика от равновесия он колеблется в вертикальной плоскости и за время t совершает N колебаний. Определите значение величины, обозначенной *. Во сколько раз изменится период колебаний такого маятника при увеличении длины нити в α раз? Во сколько раз изменится период колебаний при увеличении массы грузика в β раз?
5 вариант
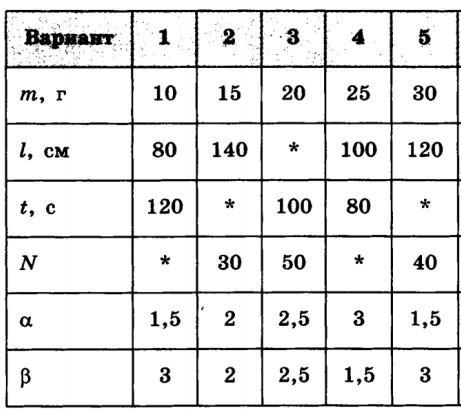
Ответы
Ответ:
Объяснение:
Так как по условию грузик небольшой, то его размерами можно пренебречь и считать его материальной точкой. Так как по условию нить - лёгкая и нерастяжимая, то её массой и упругими силами можно пренебречь. Тогда колеблющийся грузик можно считать математическим маятником. Период колебаний такого маятника T=2*π*√(l/g), где l - длина нити, g - ускорение свободного падения. Так как период не зависит от массы грузика, то при увеличении его массы в β раз период не изменится. Если длину нити увеличить в α раз, то её длина станет равной l1=l*α, и тогда период колебаний станет равным T1=2*√(l1/g)=2*π*√(l*α/g). Отсюда T1/T=√α, т.е. период колебаний увеличится в √α раз. Если известно время t N колебаний, то N=t/T=(t*√g)/(2*π*√l). Если известно число колебаний N, то время t=T*N=2*π*N*√(l/g). Если известны N и t, то l=t²*g/(4*π²*N²).