Предмет: Математика,
автор: Ternov21
Помогите пожалуйста решить примеры.
Приложения:
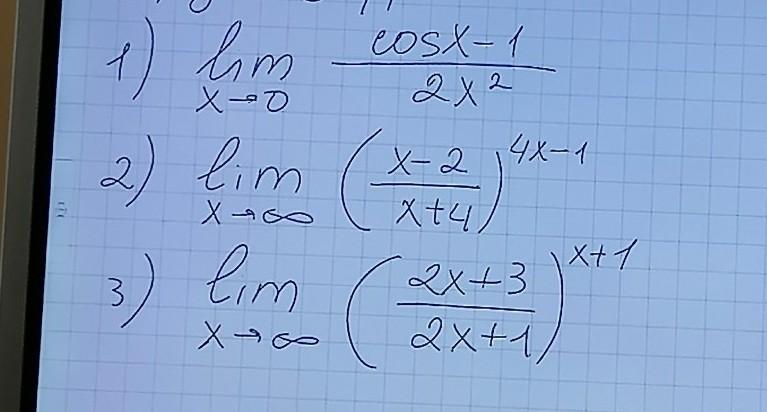
Ternov21:
нет просто главное решите.
какой? Это не ответ
Ответы
Автор ответа:
1
Ответ:решение на фото
Пошаговое объяснение:
Приложения:
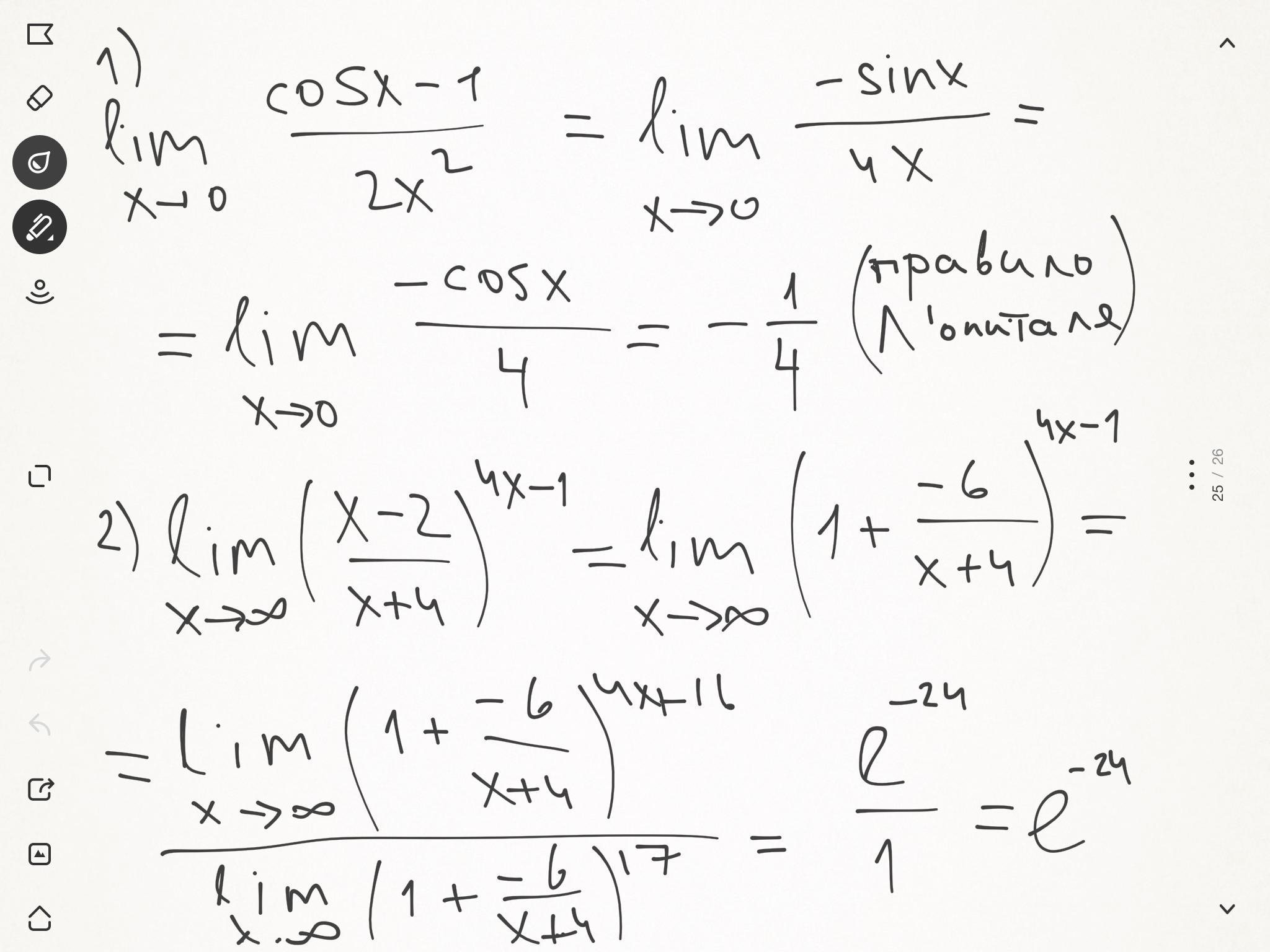
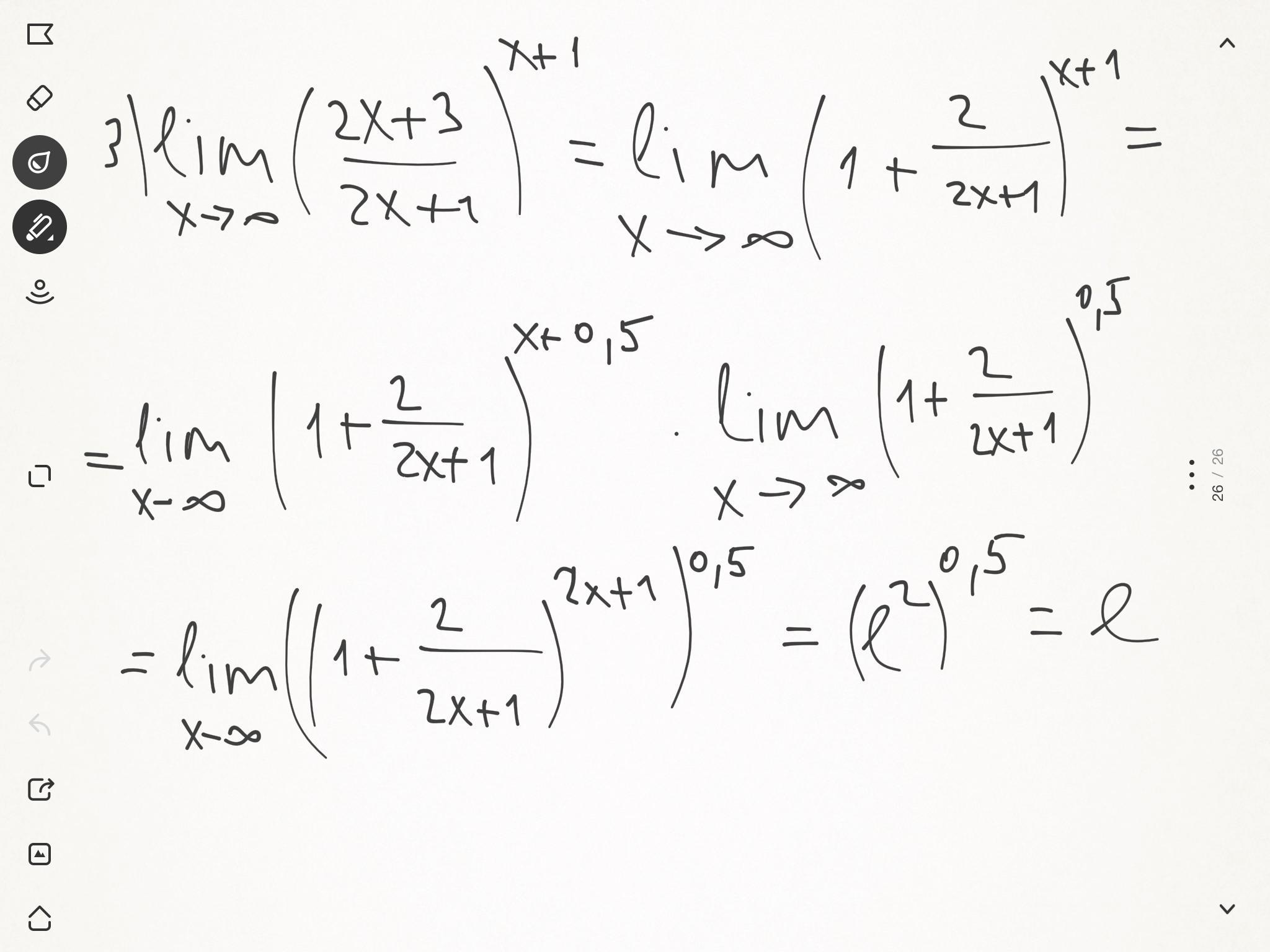
Автор ответа:
1
Ответ:
помогите решить примеры последние
самый первый вопрос
Похожие вопросы
Предмет: Русский язык,
автор: valeragrigorev14
Предмет: Английский язык,
автор: sehunluhan8835
Предмет: Русский язык,
автор: Englishland
Предмет: Русский язык,
автор: karina00745
Предмет: Русский язык,
автор: qazplm17