Предмет: Алгебра,
автор: Аноним
Помогите пожалуйста решить, Нужно найти производную
Приложения:
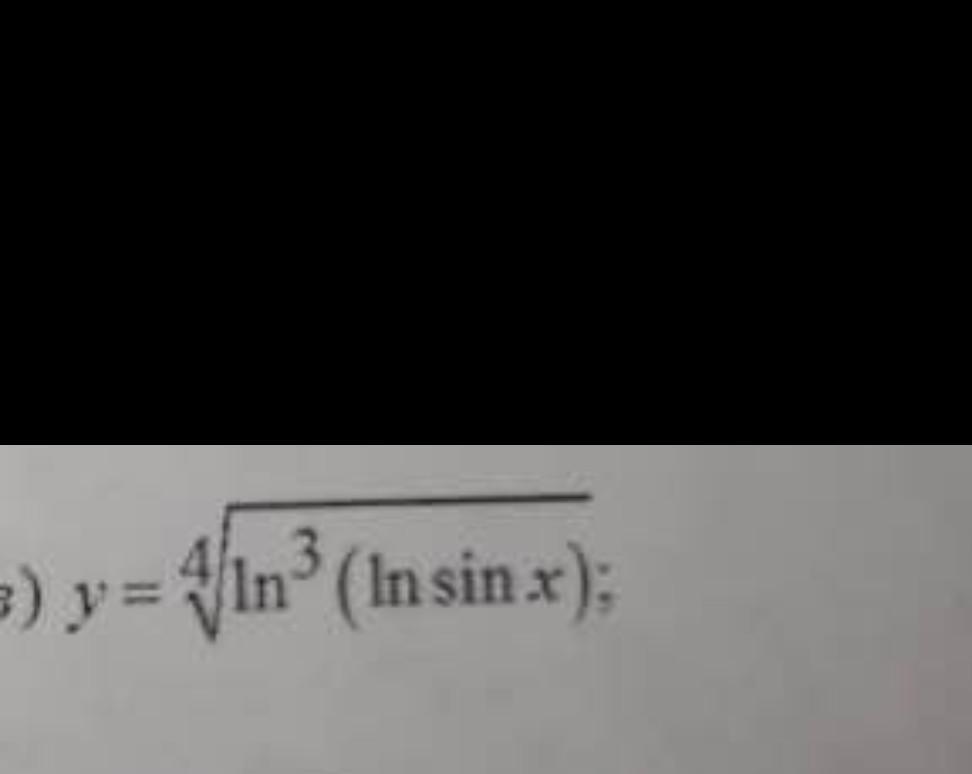
axatar:
Он "потерял" в функции один из логарифмов
Ответы
Автор ответа:
0
Ответ:
Объяснение:
Нужно знать:
а) Табличные производные от функций
б) Формулу производной от сложной функции:
Вычислим производную от функции:
Похожие вопросы
Предмет: Русский язык,
автор: аяз7
Предмет: Русский язык,
автор: натали823
Предмет: Окружающий мир,
автор: Котька31
Предмет: Окружающий мир,
автор: Emilia113454
Предмет: Русский язык,
автор: Anabela2228