Предмет: Математика,
автор: marcingulbicki5
Задача по правилу Лопиталя.
Понимаю что нужно записать в качестве натурального логаритма, но получаю бесконечность/0 и немогу применить теорему лопиталя
Приложения:
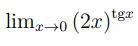
Ответы
Автор ответа:
1
Пошаговое объяснение:
Здесь ключевой момент!
Мы неопределенность [tg • ln] или [бскнч • 0]
преобразуем по формуле:
т.к. функция тангенс это же (1 / котангенс)!
Потом - правило Лопиталя.
Еще раз правило Лопиталя:
Vopoxov:
Что скажете? Надеюсь, я относительно понятно рассказал?
Благодарю! Забыл что тангенс можно так записывать
:).
Похожие вопросы
Предмет: Қазақ тiлi,
автор: кирилл926
Предмет: Русский язык,
автор: igumnova03
Предмет: Английский язык,
автор: катя2481
Предмет: История,
автор: andrew200607