Предмет: Математика,
автор: Аноним
Lim x-1 - Помогите пожалуйста
Приложения:
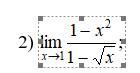
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Русский язык,
автор: lpslps347
Предмет: Русский язык,
автор: shadowbizarre
Предмет: Немецкий язык,
автор: MrStelsen
Предмет: Русский язык,
автор: azisdzhamalov