Question

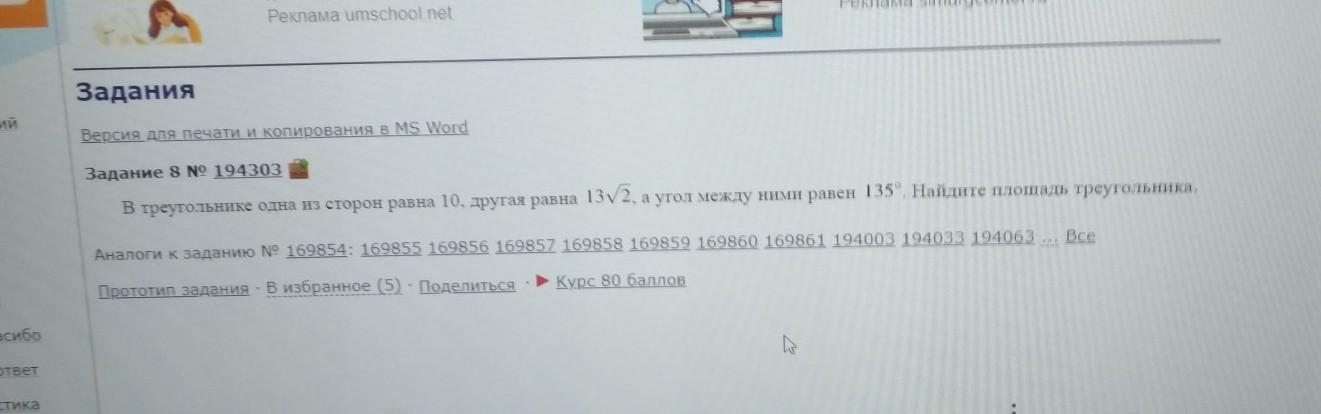
в треугольнике одна из сторон равна 10, другая равна 28, а косинус угла между ними равен 3√11/10. найдите площадь треугольника​

Answer 1

Ответ:

Объяснение:

1)

а=10ед

b=28ед

cos<(ab)=3√11/10

S=?

Решение

Тригонометрическое тождество

sin²<(ab)+cos²<(ab)=1

sin<ab=√(1-cos²<(ab))=√(1-(3√11/10)²)=

=√(1-99/100)=√(100/100-99/100)=

=√(1/100)=1/10

S=1/2*a*b*sin<(ab)=1/2*10*28*1/10=14ед²

Ответ: 14ед²

2)

а=10ед

b=13√2ед.

<(ab)=135°

sin<(ab)=sin135°=sin45°=√2/2

S=?

Решение

S=1/2*a*b*sin<(ab)=1/2*10*13√2*√2/2=65ед²

Ответ: 65ед²