плиз помогите, даю 50 баллов
Ответы
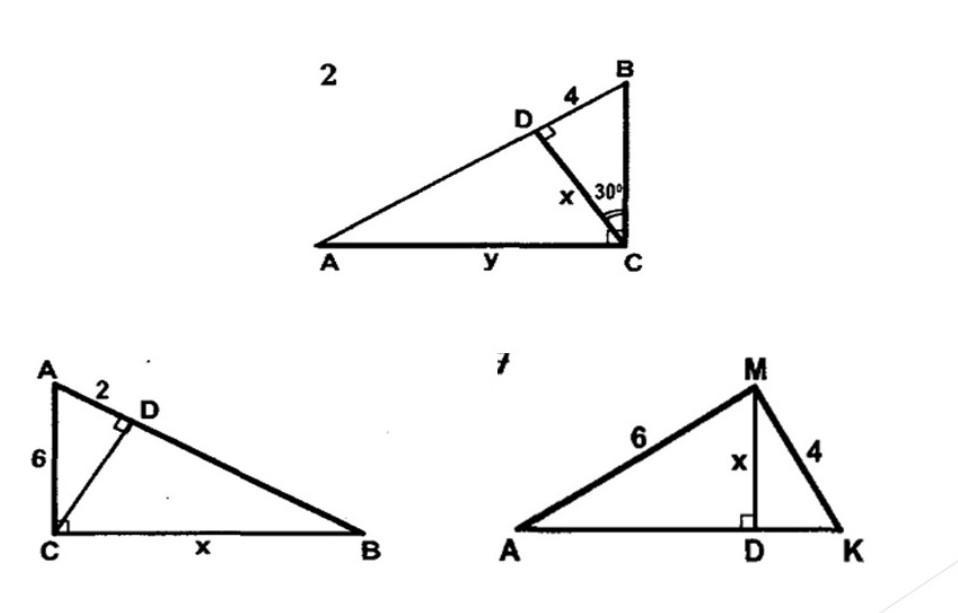
Ответ: Верхний треугольник y = 8√3; x = 4√3
Треугольник нижний левый x = 12√2.
Треугольник нижний правый x = 18/√13
Объяснение: Верхний треугольник.
Так как ΔCDB - прямоугольный то в нем против <30° лежит катет равный половине гипотенузы. Значит CB = 2DB = 2*4 = 8.
Треугольники CDB и ACB - подобны. Тогда можно записать соотношение CB/DB = AB/CB. Отсюда АВ = СВ²/DB = 8²/4 = 64/4= 16. По теореме Пифагора найдем y = АС АС² = АВ² - СВ². Отсюда АС= √(АВ² - СВ²) = √(16² - 8²) = √192 = √64*3 =
По этой же теореме найдем х =CD CD = √(СВ² - DB²) = √(64 - 16) = √48 = √16*3 = 4√3
Треугольник нижний левый.
ΔCDA подобен ΔABC. Из подобия АВ/АС = АС/AD. Отсюда АВ = АС²/AD = 6²/2 = 36/2 = 18. По теореме Пифагора Х = √(АВ² - АС²) = √(18² - 6²) = √(324 - 36) = √288 = √8*36 = √4*2*36 = 2*6*√2 = 12√2.
Треугольник нижний правый
По теореме Пифагора АК = √(АМ² + МК²) = √(6² + 4²) = √(36 + 16) = √52 = √4*13 = 2√13
Δ АМК подобен ΔMDK Тогда выполняется соотношение: АК/АМ = АМ/МD Отсюда МD = Х = АМ²/АК = 6²/2√13 = 36/2√13 = 18/√13