Предмет: Алгебра,
автор: danya111839
используйте метод вспомогательного аргумента покажите что уравнение.... помогите пожалуйста....
Приложения:
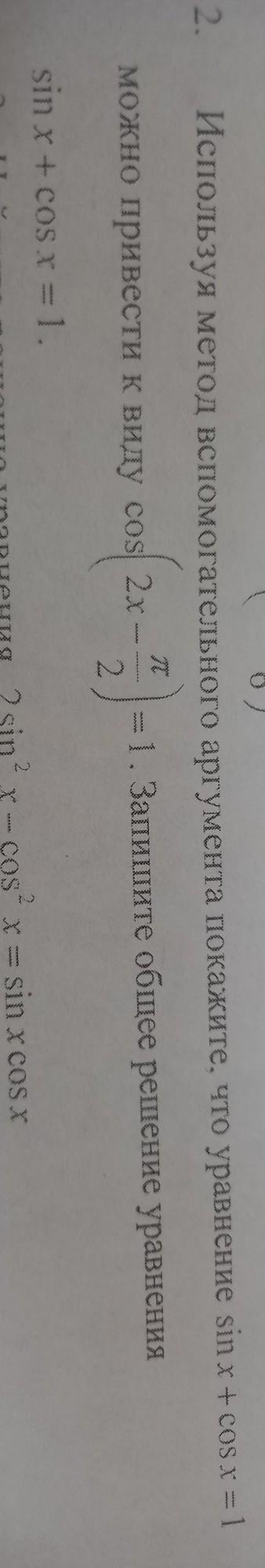
Ответы
Автор ответа:
1
Ответ:
Как видим, нельзя выражение (sinx+cosx) привести к выражению вида сos(2х-П/2) .
Похожие вопросы
Предмет: Қазақ тiлi,
автор: ятвояненовесть
Предмет: Технология,
автор: Reynikova042
Предмет: Русский язык,
автор: vlabic5455
Предмет: Алгебра,
автор: данил951
Предмет: Литература,
автор: pasykartem174