Предмет: Математика,
автор: sarastyles1401
ПОЖАЛУЙСТА ПОМОГИТЕ РЕШИТЬ СРОЧНО!!!!!
Приложения:
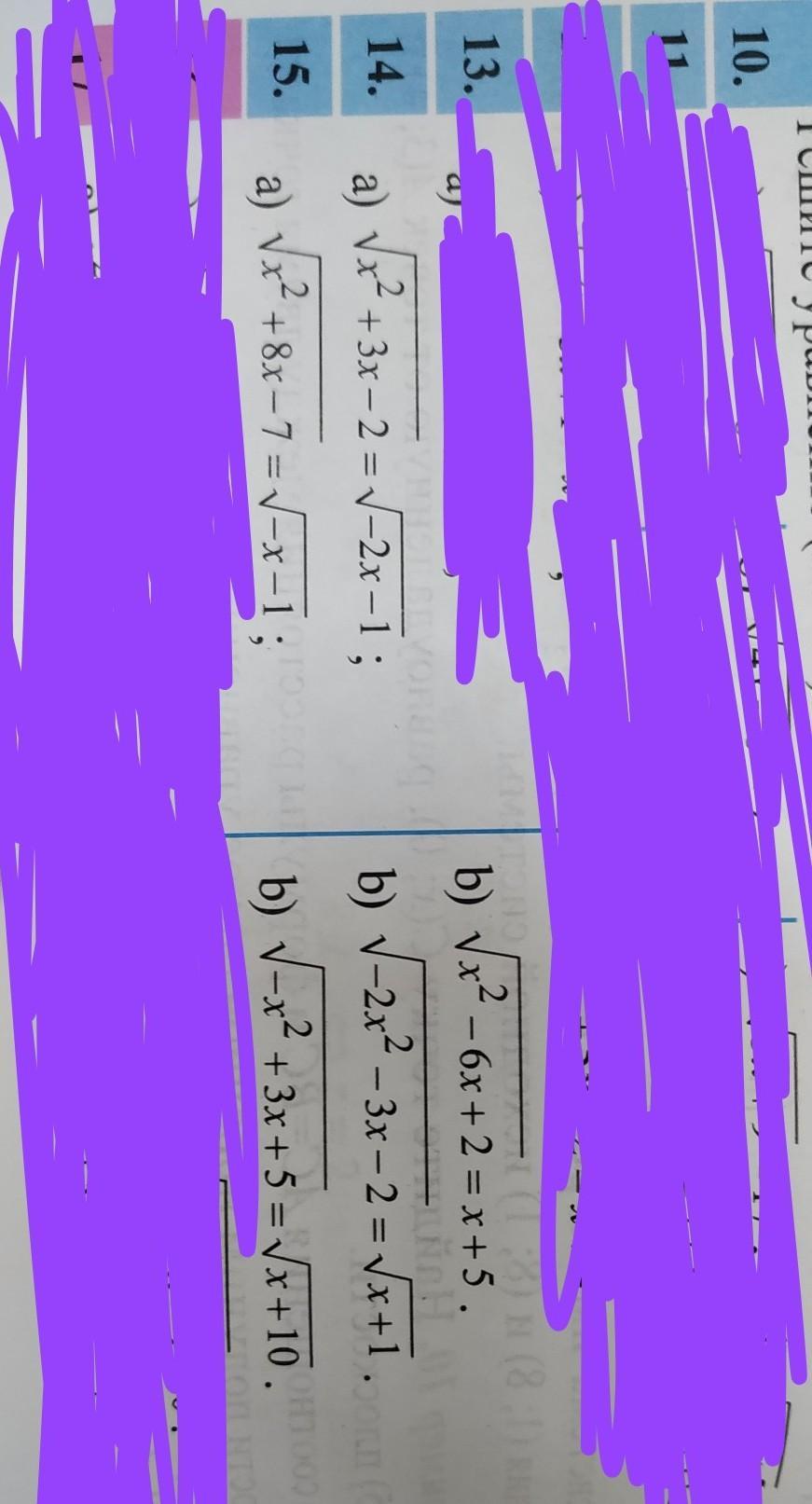
Ответы
Автор ответа:
1
Ответ:
Нет решений, так как дискриминант < 0
Нет решений, так как дискриминант < 0
Похожие вопросы
Предмет: Қазақ тiлi,
автор: xzhanka
Предмет: Технология,
автор: nekto7
Предмет: Английский язык,
автор: Соньша
Предмет: Алгебра,
автор: ArrowoffPaiN
Предмет: Русский язык,
автор: Chsd