Предмет: Алгебра,
автор: gulbahor213
Пожалуйста помогите срочно!!!!!
Приложения:
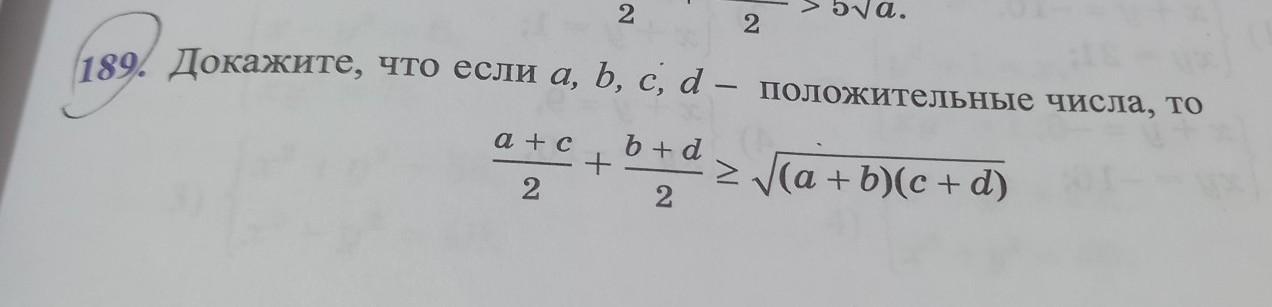
Ответы
Автор ответа:
1
Ответ:
Ч.т.д
Объяснение:
1) Преобразуем левую часть уравнения к виду ;
2) Напишем ОДЗ (Область Допустимых Значений) - подкоренное выражение всегда больше или равно нулю, так что
3) Ну раз a, b, c, d > 0, то a + b > 0 и c + d > 0, следовательно
4) Предположим, что неравенство верно, значит мы должны получить его решения. Умножим обе части на два и возведём обе части в квадрат поскольку и левая и правая часть > 0; Получим неравенство вида
5) Разложим на множители и перенесём всё в левую часть, приведём подобные:
6)
Что верно при любых числах a, b, c, d. Ч.т.д.
Похожие вопросы
Предмет: Английский язык,
автор: чашпм
Предмет: Окружающий мир,
автор: окся78
Предмет: Русский язык,
автор: evalina2007
Предмет: Математика,
автор: kristinadombro
Предмет: Литература,
автор: ISSTA