Предмет: Геометрия,
автор: dmytro007
Диаметр шара, равный 30 см, представляет собой ось цилиндра, у которого радиус основания равен 12 см. Найдите объем части шара, содержащейся внутри цилиндра
Діаметр кулі, що дорівнює 30 см, є віссю циліндра, у якого радіус основи дорівнює 12 см. Знайдіть об'єм частини кулі, що міститься всередині циліндра
Приложения:
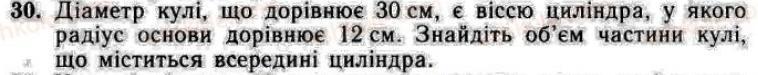
Ответы
Автор ответа:
2
Ответ: Объем шарового сегмента опущенного в цилиндр = π*468 см³
Объяснение: Дано:
Диаметр шара = 30 см тогда его радиус R = 15
Радиус основания цилиндра r = 12см
Найти объем шарового сегмента, опушенного в цилиндр V - ?
Смотрите рисунок. Что бы найти объем надо найти размер h - глубину погружения шара. По теореме Пифагора R² = r² + (R-h)² Получили квадратное уравнение: h² - 2Rh + r² = 0
h1,2 = (2R+-√4R² - 4r²)/2 = (2R+-2√R²-r²)/2 h = 6 см
Объем шарового сегмента найдем по формуле V = π*h²(R - h/3) = π*468 см³
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: h6ygtrfbdju
Предмет: Русский язык,
автор: jukhtenaloOskon
Предмет: Русский язык,
автор: xxx93
Предмет: Математика,
автор: dasha14100
Предмет: Другие предметы,
автор: mencelelizaveta3