Предмет: Алгебра,
автор: PizzaOneLove
Помогите с производными
Приложения:
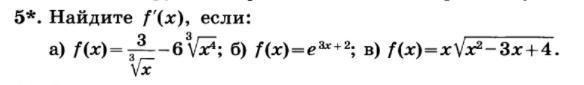
Ответы
Автор ответа:
1
PizzaOneLove:
Большое спасибо!
Пожалуйста
У меня в профиле еще одно задание по производным, даю 100 баллов! Прошу помощь
Похожие вопросы
Предмет: Русский язык,
автор: ледикри
Предмет: Русский язык,
автор: ahmadjonote
Предмет: Русский язык,
автор: шгаправжлдо
Предмет: Математика,
автор: den4589
Предмет: Русский язык,
автор: inostrankacom