срочно
даю 20 балов
заранее спасибо
Ответы
Объяснение:
под конец формула сокращения


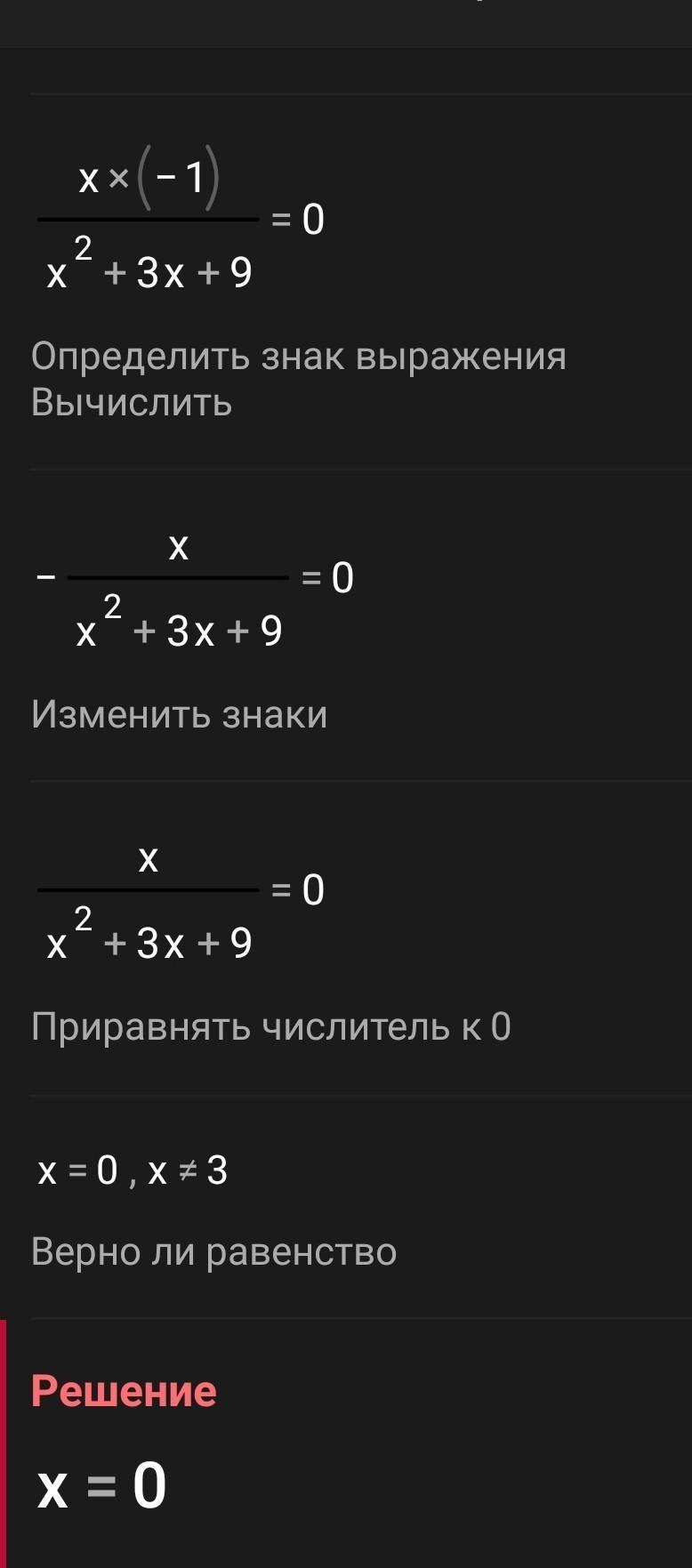
Ответ:
=0
=-3
Объяснение:
Раскладываем первый знаменатель по формуле сокращенного умножения (разность кубов): -27= (х-3)(
+3х+9), находим ОДЗ для этого знаменателя, чтобы не пришлось делить на 0.(х-3)(
+3х+9)
0
тогда х-30 -> x
3
x^{2}+3x+90 -> уравнение решений не имеет так как дискриминант меньше 0. Поэтому остается отбросить только х = 3, если этот корень появится в решении. Второй знаменатель точно такой же как один из сомножителей первого знаменателя, поэтому ОДЗ будет таким, что х будет любым так как
+3х+9
0 при любом х. Правую часть уравнения переносим влево меняя знак на противоположный, т.е. на (-) и приводим все к общему знаменателю:
-27. В числителе приводим общие слагаемые и получаем уравнение
+3х=0 оно имеет два корня
=0 и
=-3. Так как ни один из корней не равен 3, то оставляем оба из них.