Предмет: Математика,
автор: jbyxmtt4fp
Знайти точки максимуму функції y=3+8x^2-x^4
Приложения:
Ответы
Автор ответа:
0
Решение:
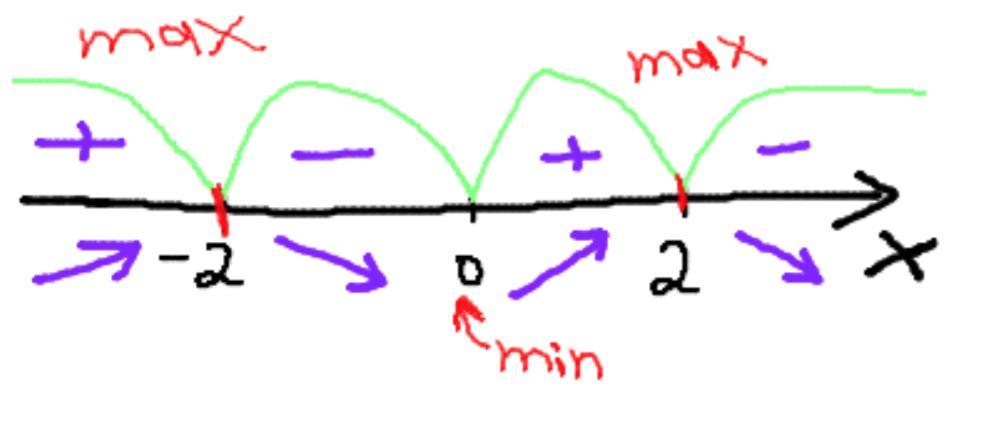
1) Знаходимо першу похідну функції::
2) Прирівнюємо першу похідну до нуля:
3) Потім підставляємо будь-які значення x в першу похідну в межах значень (до, після або між) :
Максимуми функції: -2 i 2, то тобто варіант відповіді Б.
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: irinashheglova
Предмет: Русский язык,
автор: zpebo
Предмет: Русский язык,
автор: Elena220511
Предмет: Математика,
автор: igul9704
Предмет: Химия,
автор: scherbinadarina