Предмет: Алгебра,
автор: кримcoн
Найти производную функции
Приложения:
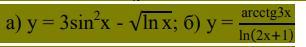
Ответы
Автор ответа:
0
Ответ:
Похожие вопросы
Предмет: Русский язык,
автор: настя3671
Предмет: Окружающий мир,
автор: Маша81111
Предмет: Русский язык,
автор: ксюшка106
Предмет: Математика,
автор: alexei502