Question

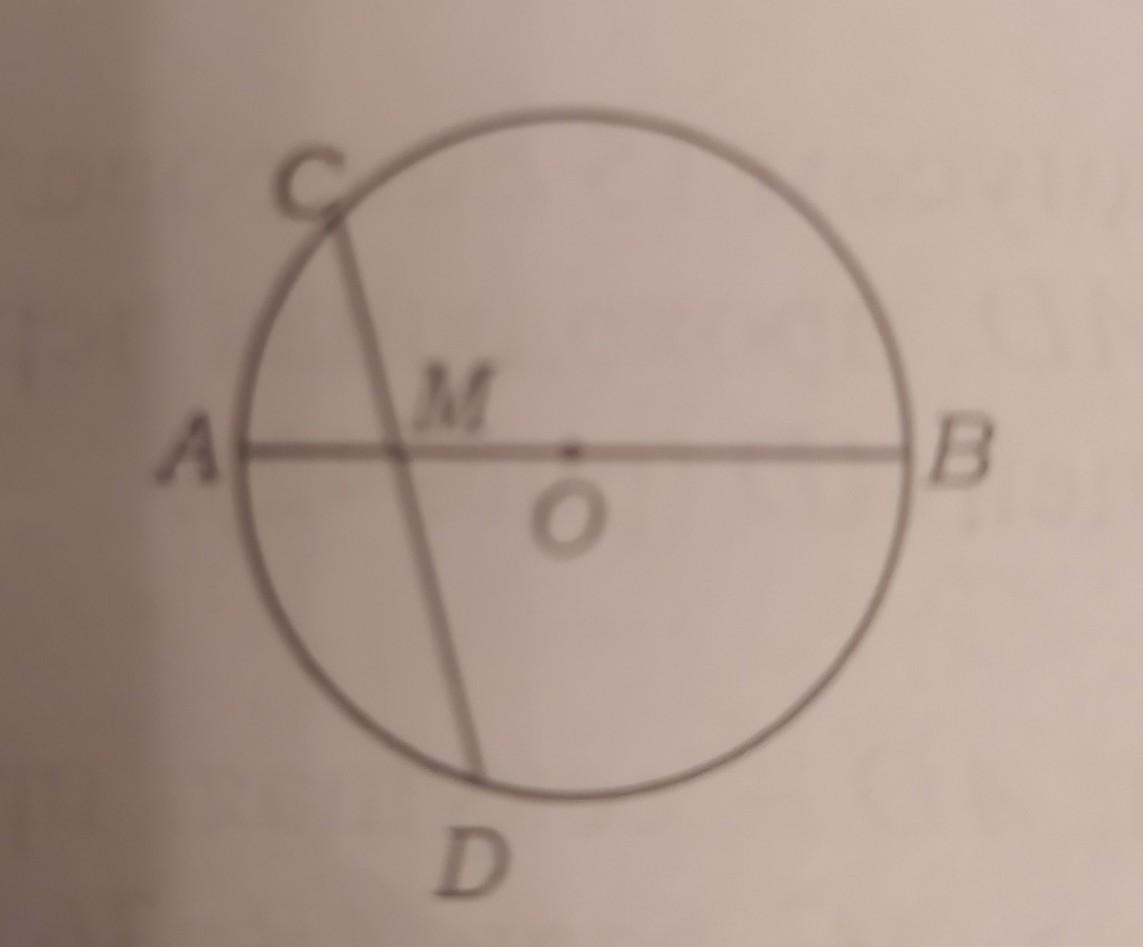
В окружности диаметр AB пересекает хорду CD в точке М. Найдите длину отрезков AM и MB, если СМ=9 см, MD=16 см и OM=5 см​

Answer 1

Ответ:    AM = 8 см,   MB = 18 см.

Объяснение:  Для пересекающихся хорд выполняется соотношение:

АМ * МВ = СМ * МД          (1)

Примем АМ = х.   МВ = ОВ + ОМ . Но, ОВ = АО и  равно х+ОМ. Таким образом, МВ = х + 2ОМ = х + 2*5 = х + 10.

Подставим в соотношение (1) числовые значения имеем: х*(х+10) = 9*16. Получили квадратное уравнение: х² + 10х - 144 = 0.

Решая уравнение найдем х1 = - 18 (решением задачи не является)

х2 = 8 см.  Отрезок МВ = х + 10 = 8 + 10 = 18 см.

Проверим АМ * МВ = 8*18 = 144;    СМ * МД  = 9*16 = 144. Задача решена

верно.