Question

Сторони паралелограма відносяться як 1:2. Знайди сторони паралелограма, якщо його діагоналі дорівнюють 18см і 26см.

Answer 1

Відповідь:

10, 20

Пояснення:

Нехай а та b сторони паралелограма і b=2a

2(a²+b²)=d1²+d2²

2(a²+4a²)=324+676

10a²=1000

a²=100

a=10, b=20

Answer 2

Ответ:

АВ = 10 см

ВС = 20 см

Объяснение:

Стороны параллелограмма относятся как 1:2. Найди стороны параллелограмма, если его диагонали равны 18см и 26см.

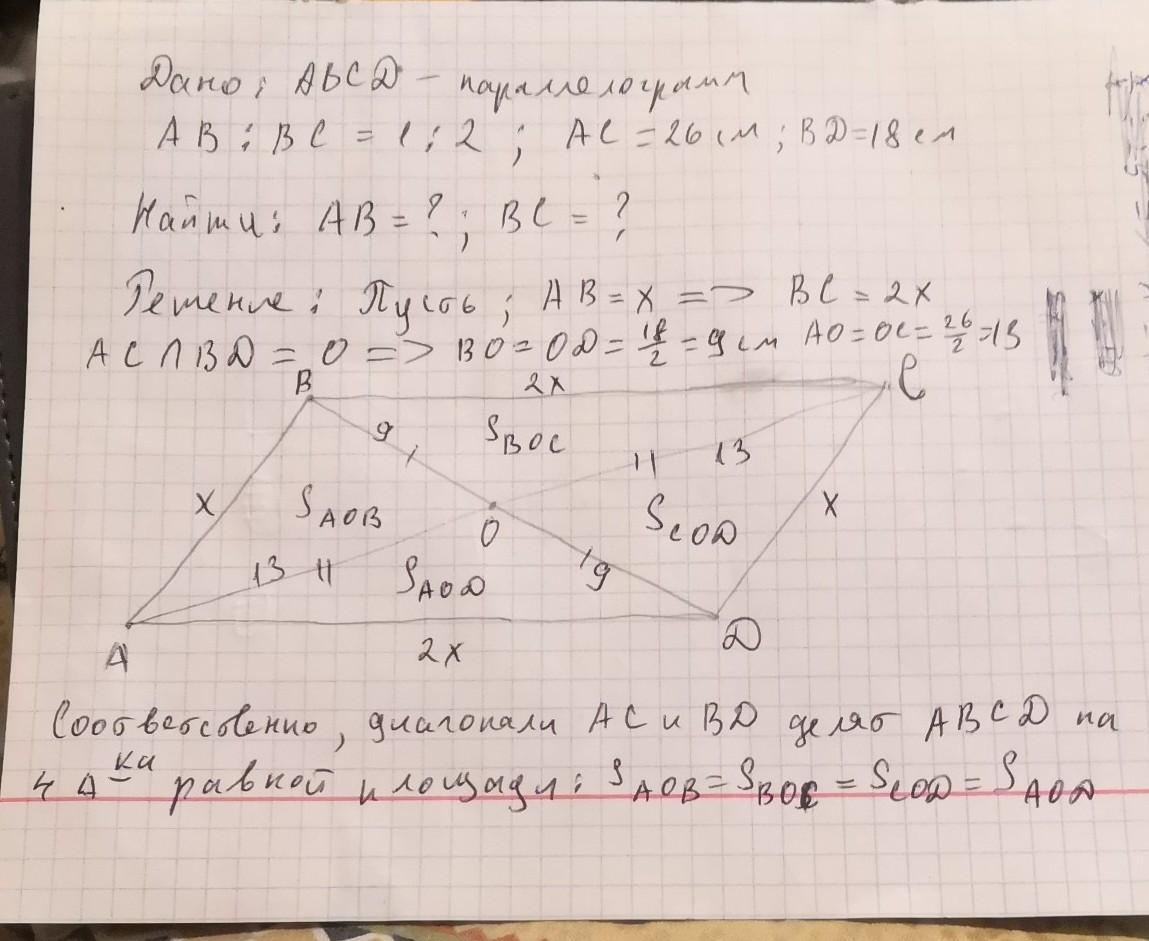
Дано:

ABCD - параллелограмм.

AB:BC = 1:2

BD = 18 см, AC = 26 см.

Найти:

АВ = ?; ВС = ?

Решение:

Обозначим короткую сторону параллелограмма АВ за х. Тогда длинная сторона BC будет равна 2х.

Т.к. АС и BD - диагонали параллелограмма, =>

т. пересечения делит их пополам:

$AC \cap BD {=} O \: {= }{ >} ; \\ AO = OC = \frac{18}{2} =9; \\ BO= OD= \frac{26}{2} = 13.$

Рассмотрим ∆АОВ и ∆COВ

$S_{AOB} = \frac{1}{2}AO\cdot{h}\\ S_{COB} = \frac{1}{2}CO\cdot{h}$

Так как из одной вершины параллелограмма на диагональ можно опустить только одну высоту, AO = CO => S(∆АОВ) = S(∆COВ)

Аналогично доказывается равенство всех четырех ∆ков.

А раз площади ∆АОВ и ∆COВ равны, то можно применить формулу Герона, где приравняем площади треугольников S(∆АОВ) = S(∆COВ)

- S1(∆АОВ): AO = 13 cm, BO = 9 cm, AB = х cm

- S2(∆CОВ): BO = 9 cm, CO = 13, BC= 2х cm

Формула Герона:

$S = \sqrt{p(p-a)(p-b)(p-c)}$

где:

для S1:

$a=9, \: b=13, \: c=x \: = > \\ p = \frac{9 + 13 + x}{2} = 11 + \frac{x}{2} , \\ p - a=11 + \frac{x}{2} - 9 =\frac{x}{2} + 2 , \\ p - b=11 + \frac{x}{2} - 13 = \frac{x}{2} - 2, \\ p - c=11+ \frac{x}{2} - x = 11 - \frac{x}{2}$

Для S2:

$a=9, \: b=13, \: c=2x \: = > \\ p = \frac{9 + 13 + 2x}{2} = 11 + {x} , \\ p - a=11 + x - 9 =x+ 2 , \\ p - b=11 + {x}- 13 = x - 2, \\ p - c=11+ {x}- 2x = 11 - {x}$

Т.к. S1 = S2 то

$\sqrt{(11 + \tfrac{x}{2}) ( \tfrac{x}{2}) + 2)( \tfrac{x}{2} - 2)(11 - \tfrac{x}{2})} = \\ = \sqrt{(11 + x)(x + 2)(x - 2)(11 - x)}$

Т.к. длины сторон не могут быть отрицательными, равенство корней обозначает и равенство подкоренных выражений: (заметим формулу разности кважратов)

${(11 + \tfrac{x}{2}) ( \tfrac{x}{2} + 2)( \tfrac{x}{2} - 2)(11 - \tfrac{x}{2})} = \\ = {(11 + x)(x + 2)(x - 2)(11 - x)} \\ \\ {(11 + \tfrac{x}{2})(11 - \tfrac{x}{2}) ( \tfrac{x}{2}+ 2)( \tfrac{x}{2} - 2)} = \\ = {(11 + x)(11 - x)(x + 2)(x - 2)} \\ \small(121 {- } \frac{ {x}^{2} }{4} )( \frac{ {x}^{2} }{4} - 4 ) = (121{ -} {x}^{2} )( {x}^{2} { -} 4)$

После преобразования сделаем замену:

$y = \frac{ {x}^{2} }{4} < = > {x}^{2} = 4y$

$\small(121 {- } y )( y{ -} {4} ) = (121{ -} 4y )( 4y { -} 4) \\ \small 121y{ -} {y}^{2} { +} 4y{ -} \cancel{ 484} = 484y{ -} 16 {y}^{2} { + }16y{ -} \cancel{ 484} \\ 125y - {y}^{2} = 500y - 16 {y}^{2} \\ 16 {y}^{2} - {y}^{2} + 125y - 500y = 0 \\ 15 {y}^{2} - 375y = 0 \: \: \: \: \bigg| \: ^{375 = 15 \times 25} \\ 15y(y - 25) = 0 \\ \left[ \: \large{^{y = 0} _{y = 25} } \right.$

Получили 2 варианта решения

Рассмотрим первый вариант

$\frac{ {x}^{2} }{4} = 0 < = > x = 0 \: = > x \in \cancel o$

Т.к. длина стороны > 0, => х=0 не подходит.

Второй вариант:

$\frac{ {x}^{2} }{4} = 25 < = > {x}^{2} = 1 00 \\ x_1=10; \: \: \: \cancel{x_2=-10 }$

Т.к. длина стороны должна быть положительным числом, => х=-10 не подходит.

Следовательно, единственный подходящий вариант: х = 10

А значит

Ответ:

АВ = х = 10 см

ВС = 2х = 20 см