Question

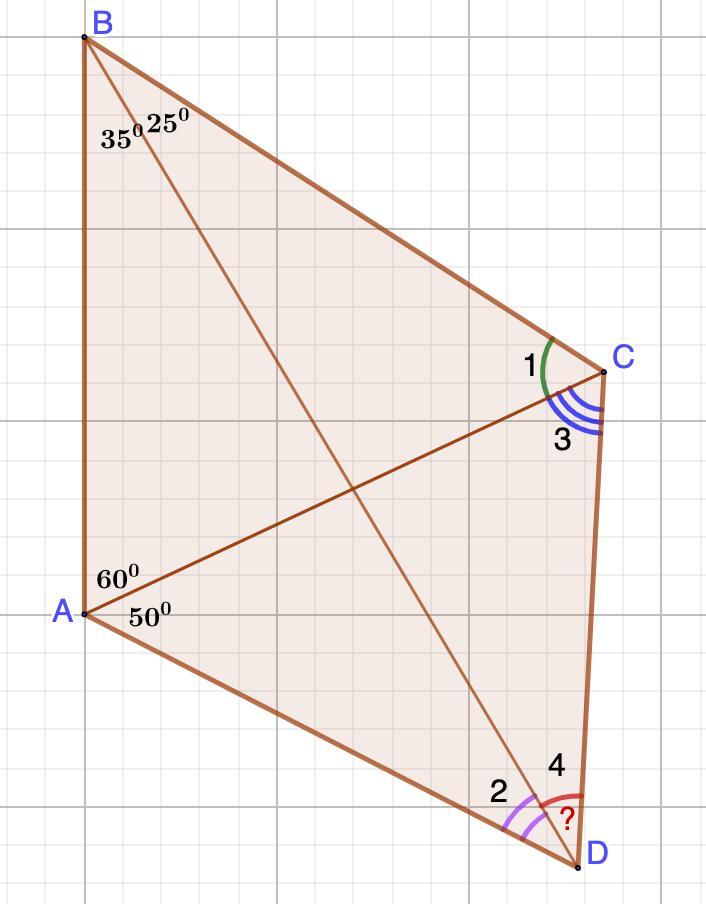
Диагональ AC выпуклого четырёх угольник ABCD образует со стороной AB угол 60°, а со стороной AD угол 50°. Диагональ BD образует со стороной AB угол 35°, а со стороной BC угол 25°. Найдите уголBDC
Пжжж

Answer 1

Ответ:

30°

Пошаговое объяснение:

Дано: ABCD - четырехугольник.

∠ABD = 35°; ∠DBC = 25°; ∠BAC = 60°; ∠CAD = 50°

Найти: ∠BDC

Решение:

1. Рассмотрим Δ АВС.

∠В = ∠АВD + ∠DBC = 35° + 25° = 60°

• Сумма углов треугольника равна 180°.

⇒ ∠1 = 180° - ∠BAC - ∠B = 180° - 60° - 60° = 60°

• Если в треугольнике все углы равны 60°, то этот треугольник равносторонний.

⇒ АВ = ВС = АС.

2) Рассмотрим ΔABD.

∠A = ∠BAC + ∠CAD = 60° + 50° = 110°

∠2 = 180° - ∠A - ∠ABD = 180° - 110° - 35° = 35°

• Если у треугольника два угла равны, то этот треугольник — равнобедренный.

⇒ AB = AD

3. Рассмотрим ΔАСD.

AB = AD (п.2)

АВ = АС (п.1)

⇒ AD = AC

ΔАСD - равнобедренный (по определению)

• Углы при основании равнобедренного треугольника равны.

⇒ ∠D = ∠3 = (180°-∠DAC) : 2 = (180° - 50°) :2 = 65°

4. ∠BDC = ∠D - ∠2 = 65° - 35° = 30°