Предмет: Алгебра,
автор: sinus348
Даю 25 баллов, 6.14 задание. Срочно!
Приложения:
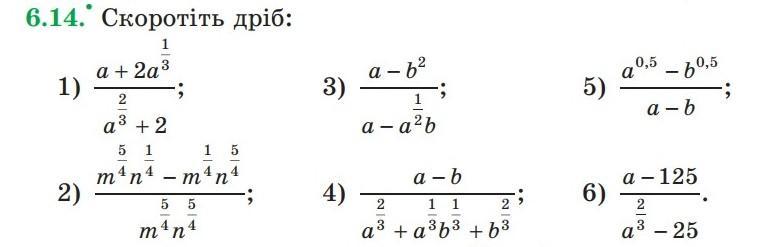
Ответы
Автор ответа:
0
Ответ:
Похожие вопросы
Предмет: Русский язык,
автор: jen4
Предмет: Русский язык,
автор: Юлия121111111
Предмет: Русский язык,
автор: костя316
Предмет: Математика,
автор: cska50
Предмет: Литература,
автор: sadakov03