Question

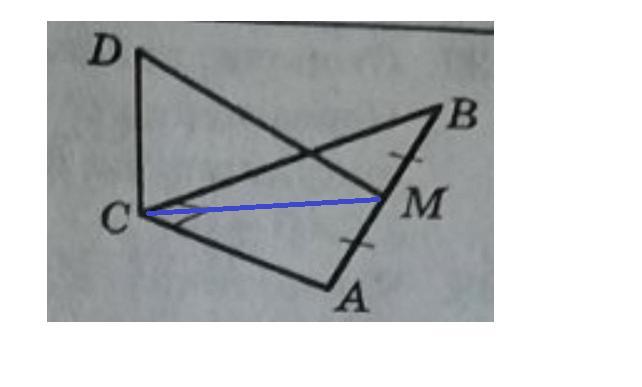
У трикутнику авс відомо що кут с 90 ас 6 вс 8, точка М - середина ab. Пряма dc перпендикудярна до площини abc, dc=12см. Знайдіть відрізок dm.

Answer 1

Ответ:

13 см

Объяснение:

Из ΔАВС по теореме Пифагора:

АВ = √(АС² + ВС²) = √(6² + 8²) = √(36 + 64) = √100 = 10 см

Медиана прямоугольного треугольника, проведенная к гипотенузе, равна ее половине:

СМ = 1/2 АВ = 1/2 · 10 = 5см

ΔDCM: ∠DCM = 90°  (если прямая перпендикулярна плоскости, то она перпендикулярна любой прямой в этой плоскости), по теореме Пифагора:

DM = √(DC² + CM²) = √(12² + 5²) = √(144 + 25) = √169 = 13 см